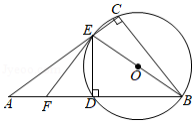
如图所示, 是 的直径,点 、 是 上不同的两点,直线 交线段 于点 、交过点 的直线 于点 ,若 ,且 .
(1)求证:直线 是 的切线;
(2)连接 、 、 、 ,若 .
①求证: ;
②过点 作 ,交线段 于点 ,点 为线段 的中点,若 ,求线段 的长度.

如图所示,在平面直角坐标系 中,一次函数 的图象 与函数 的图象(记为 交于点 ,过点 作 轴于点 ,且 ,点 在线段 上(不含端点),且 ,过点 作直线 轴,交 于点 ,交图象 于点 .
(1)求 的值,并且用含 的式子表示点 的横坐标;
(2)连接 、 、 ,记 、 的面积分别为 、 ,设 ,求 的最大值.

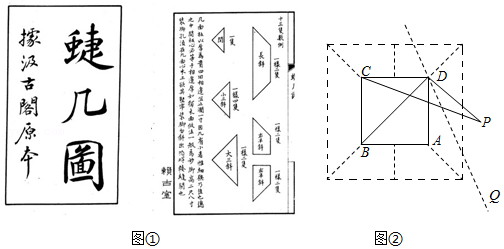
《蝶几图》是明朝人戈汕所作的一部组合家具的设计图
"  "为"蜨",同"蝶"
,它的基本组件为斜角形,包括长斜两只、右半斜两只、左半斜两只、闺一只、小三斜四只、大三斜两只,共十三只(图①中的"樣"和"隻"为"样"和"只"
.图②为某蝶几设计图,其中
和
为"大三斜"组件
"一樣二隻"的大三斜组件为两个全等的等腰直角三角形),已知某人位于点
处,点
与点
关于直线
对称,连接
、
.若
,则
度.
"为"蜨",同"蝶"
,它的基本组件为斜角形,包括长斜两只、右半斜两只、左半斜两只、闺一只、小三斜四只、大三斜两只,共十三只(图①中的"樣"和"隻"为"样"和"只"
.图②为某蝶几设计图,其中
和
为"大三斜"组件
"一樣二隻"的大三斜组件为两个全等的等腰直角三角形),已知某人位于点
处,点
与点
关于直线
对称,连接
、
.若
,则
度.
我们不妨约定:在平面直角坐标系中,若某函数图象上至少存在不同的两点关于 轴对称,则把该函数称之为“ 函数”,其图象上关于 轴对称的不同两点叫做一对“ 点”.根据该约定,完成下列各题.
(1)若点 与点 是关于 的“ 函数” 的图象上的一对“ 点”,则 , , (将正确答案填在相应的横线上);
(2)关于 的函数 , 是常数)是“ 函数”吗?如果是,指出它有多少对“ 点”如果不是,请说明理由;
(3)若关于 的“ 函数” ,且 , , 是常数)经过坐标原点 ,且与直线 , ,且 , 是常数)交于 , , , 两点,当 , 满足 时,直线 是否总经过某一定点?若经过某一定点,求出该定点的坐标;否则,请说明理由.
在一次数学活动课上,某数学老师将 共十个整数依次写在十张不透明的卡片上(每张卡片上只写一个数字,每一个数字只写在一张卡片上,而且把写有数字的那一面朝下).他先像洗扑克牌一样打乱这些卡片的顺序,然后把甲,乙,丙,丁,戊五位同学叫到讲台上,随机地发给每位同学两张卡片,并要求他们把自己手里拿的两张卡片上的数字之和写在黑板上,写出的结果依次是:甲:11;乙:4;丙:16;丁:7;戊:17.根据以上信息,下列判断正确的是
| A. |
戊同学手里拿的两张卡片上的数字是8和9 |
| B. |
丙同学手里拿的两张卡片上的数字是9和7 |
| C. |
丁同学手里拿的两张卡片上的数字是3和4 |
| D. |
甲同学手里拿的两张卡片上的数字是2和9 |
阅读下面的材料:
如果函数 满足:对于自变量 取值范围内的任意 , ,
(1)若 ,都有 ,则称 是增函数;
(2)若 ,都有 ,则称 是减函数.
例题:证明函数 是增函数.
证明:任取 ,且 , .
则 .
且 , ,
, .
,即 , .
函数 是增函数.
根据以上材料解答下列问题:
(1)函数 , (1) , (2) , (3) , (4) ;
(2)猜想 是 函数(填“增”或“减” ,并证明你的猜想.
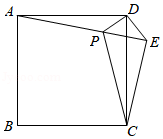
如图,在正方形 外取一点 ,连接 , , ,过点 作 的垂线交 于点 ,若 , .下列结论:① ;② ;③点 到直线 的距离为 ;④ ,其中正确结论的序号为 .
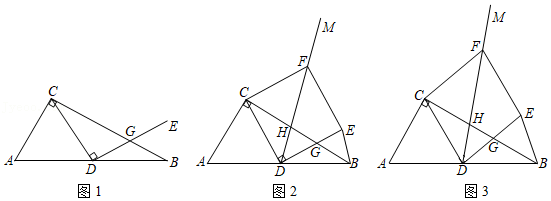
如图,在 中, , ,点 为 的中点,连接 ,将线段 绕点 顺时针旋转 得到线段 ,且 交线段 于点 , 的平分线 交 于点 .
(1)如图1,若 ,则线段 与 的数量关系是 , ;
(2)如图2,在(1)的条件下,过点 作 交 于点 ,连接 , .
①试判断四边形 的形状,并说明理由;
②求证: ;
(3)如图3,若 , ,过点 作 交 于点 ,连接 , ,请直接写出 的值(用含 的式子表示).
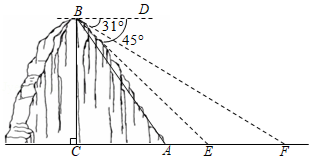
某镇为创建特色小镇,助力乡村振兴,决定在辖区的一条河上修建一座步行观光桥.如图,该河旁有一座小山,山高 ,坡面 的坡度 (注:坡度 是指坡面的铅直高度与水平宽度的比),点 、 与河岸 、 在同一水平线上,从山顶 处测得河岸 和对岸 的俯角分别为 , .
(1)求山脚 到河岸 的距离;
(2)若在此处建桥,试求河宽 的长度.(结果精确到
(参考数据: , ,
如图,在 中, , 的垂直平分线分别交 、 于点 、 , , 为 的外接圆,过点 作 的切线 交 于点 ,则下列结论正确的是 (写出所有正确结论的序号)
① ;
② ;
③若 ,则 的长为 ;
④ ;
⑤若 ,则 .
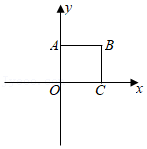
定义:我们将顶点的横坐标和纵坐标互为相反数的二次函数称为"互异二次函数".如图,在正方形 中,点 ,点 ,则互异二次函数 与正方形 有交点时 的最大值和最小值分别是
| A. |
4, |
B. |
, |
C. |
4,0 |
D. |
, |
已知关于 的二次函数 (实数 , 为常数).
(1)若二次函数的图象经过点 ,对称轴为 ,求此二次函数的表达式;
(2)若 ,当 时,二次函数的最小值为21,求 的值;
(3)记关于 的二次函数 ,若在(1)的条件下,当 时,总有 ,求实数 的最小值.
如图1, 是 的直径,点 是 上一动点,且不与 , 两点重合, 的平分线交 于点 ,过点 作 ,交 的延长线于点 .

(1)求证: 是 的切线;
(2)求证: ;
(3)如图2,原有条件不变,连接 , ,延长 至点 , 的平分线交 的延长线于点 , 的平分线交 的平分线于点 .求证:无论点 如何运动,总有 .
试题篮
()