如图,在矩形 中, , ,点 是边 的中点,反比例函数 的图象经过点 ,交 边于点 ,直线 的解析式为 .
(1)求反比例函数 的解析式和直线 的解析式;
(2)在 轴上找一点 ,使 的周长最小,求出此时点 的坐标;
(3)在(2)的条件下, 的周长最小值是 .

如图,点 是反比例函数 图象上一点,过点 分别向坐标轴作垂线,垂足为 , .反比例函数 的图象经过 的中点 ,与 , 分别相交于点 , .连接 并延长交 轴于点 ,点 与点 关于点 对称,连接 , .
(1)填空: ;
(2)求 的面积;
(3)求证:四边形 为平行四边形.
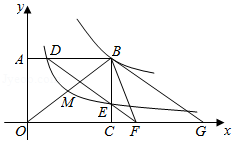
如图,已知 , ,反比例函数 的图象过点 ,反比例函数 的图象过点 .
(1)求 和 的值;
(2)过点 作 轴,与双曲线 交于点 .求 的面积.

如图所示,在平面直角坐标系 中,等腰 的边 与反比例函数 的图象相交于点 ,其中 ,点 在 轴的正半轴上,点 的坐标为 ,过点 作 轴于点 .
(1)已知一次函数的图象过点 , ,求该一次函数的表达式;
(2)若点 是线段 上的一点,满足 ,过点 作 轴于点 ,连结 ,记 的面积为 ,设 ,
①用 表示 (不需要写出 的取值范围);
②当 取最小值时,求 的值.

如图,直线y=4﹣x与双曲线y 交于A,B两点,过B作直线BC⊥y轴,垂足为C,则以OA为直径的圆与直线BC的交点坐标是 .

如图,在平面直角坐标系中, 与 轴的正半轴交于 、 两点,与 轴的正半轴相切于点 ,连接 、 ,已知 半径为2, ,双曲线 经过圆心 .
(1)求双曲线 的解析式;
(2)求直线 的解析式.

(1)阅读理解
如图,点 , 在反比例函数 的图象上,连接 ,取线段 的中点 .分别过点 , , 作 轴的垂线,垂足为 , , , 交反比例函数 的图象于点 .点 , , 的横坐标分别为 , , .
小红通过观察反比例函数 的图象,并运用几何知识得出结论:
,
由此得出一个关于 , , ,之间数量关系的命题:
若 ,则 .
(2)证明命题
小东认为:可以通过“若 ,则 ”的思路证明上述命题.
小晴认为:可以通过“若 , ,且 ,则 ”的思路证明上述命题.
请你选择一种方法证明(1)中的命题.

已知一次函数 的图象与反比例函数 的图象交于点 ,与 轴交于点 ,若 ,且 .
(1)求反比例函数与一次函数的表达式;
(2)若点 为 轴上一点, 是等腰三角形,求点 的坐标.

阅读下面的材料:
如果函数 满足:对于自变量 的取值范围内的任意 , ,
(1)若 ,都有 ,则称 是增函数;
(2)若 ,都有 ,则称 是减函数.
例题:证明函数 是减函数.
证明:设 ,
.
,
, .
.即 .
.
函数 是减函数.
根据以上材料,解答下面的问题:
已知函数 ,
,
(1)计算: , ;
(2)猜想:函数 是 函数(填“增”或“减” ;
(3)请仿照例题证明你的猜想.
如图1,点 、点 在直线 上,反比例函数 的图象经过点 .

(1)求 和 的值;
(2)将线段 向右平移 个单位长度 ,得到对应线段 ,连接 、 .
①如图2,当 时,过 作 轴于点 ,交反比例函数图象于点 ,求 的值;
②在线段 运动过程中,连接 ,若 是以 为腰的等腰三角形,求所有满足条件的 的值.
如图,过原点的直线与反比例函数 的图象交于 , 两点,点 在第一象限.点 在 轴正半轴上,连结 交反比例函数图象于点 . 为 的平分线,过点 作 的垂线,垂足为 ,连结 .若 , 的面积为8,则 的值为 .

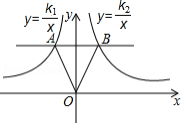
如图,在 轴上方,平行于 轴的直线与反比例函数 和 的图象分别交于 、 两点,连接 、 ,若 的面积为6,则 .
模具厂计划生产面积为4,周长为 的矩形模具.对于 的取值范围,小亮已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下:
(1)建立函数模型
设矩形相邻两边的长分别为 , ,由矩形的面积为4,得 ,即 ;由周长为 ,得 ,即 .满足要求的 应是两个函数图象在第 一 象限内交点的坐标.
(2)画出函数图象
函数 的图象如图所示,而函数 的图象可由直线 平移得到.请在同一直角坐标系中直接画出直线 .
(3)平移直线 ,观察函数图象
①当直线平移到与函数 的图象有唯一交点 时,周长 的值为 ;
②在直线平移过程中,交点个数还有哪些情况?请写出交点个数及对应的周长 的取值范围.
(4)得出结论
若能生产出面积为4的矩形模具,则周长 的取值范围为 .

小明在研究矩形面积 与矩形的边长 , 之间的关系时,得到下表数据:
|
|
0.5 |
1 |
1.5 |
2 |
3 |
4 |
6 |
12 |
|
|
12 |
6 |
4 |
3 |
2 |
|
1 |
0.5 |
结果发现一个数据被墨水涂黑了
(1)被墨水涂黑的数据为 .
(2) 与 之间的函数关系式为 ,且 随 的增大而 .
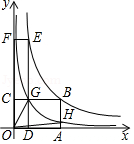
(3)如图是小明画出的 关于 的函数图象,点 、 均在该函数的图象上,其中矩形 的面积记为 ,矩形 的面积记为 ,请判断 和 的大小关系,并说明理由.
(4)在(3)的条件下, 交 于点 ,反比例函数 的图象经过点 交 于点 ,连接 、 ,则四边形 的面积为 .
试题篮
()