如图,等腰梯形ABCD的对角线长为13,点E、F、G、H分别是边AB、BC、CD、DA的中点,则四边形EFGH的周长是()
A.13 B.26 C.36 D.39
如图,在斜边为1的等腰直角三角形OAB中,作内接正方形A1B1C1D1;在等腰直角三角形OA1B1中,作内接正方形A2B2C2D2;在等腰直角三角形OA2B2中,作内接正方形A3B3C3D3…依次作下去,则第n个正方形AnBnCnDn的边长是()
A. |
B. |
C. |
D. |
在一张长12cm、宽5cm的矩形纸片内,要折出一个菱形.小华同学按照取两组对边中点的方法折出菱形EFGH(见方案一),小丽同学沿矩形的对角线AC折出∠CAE=∠CAD,∠ACF=∠ACB的方法得到菱形AECF(见方案二).
(1)你能说出小华、小丽所折出的菱形的理由吗?
(2)请你通过计算,比较小华和小丽同学的折法中,哪种菱形面积较大?
下列说法中错误的是()
| A.平行四边形的对角线互相平分 |
| B.有两对邻角互补的四边形为平行四边形 |
| C.对角线互相平分的四边形是平行四边形 |
| D.一组对边平行,一组对角相等的四边形是平行四边形 |
如图,AB是⊙O的弦,半径OC⊥AB于点D,且AB=6cm,OD=4cm。则DC的长为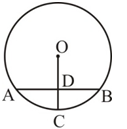
A.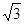 cm cm |
B.1cm | C.2cm | D.5cm |
如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是()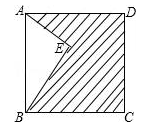
| A.48 | B.60 | C.76 | D.80 |
如图,正方形ABCD的边长为4cm,动点P、Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动,设运动时间为x(单位:s),四边形PBDQ的面积为y(单位:cm2),则y与x(0≤x≤8)之间的函数关系可用图象表示为

正n边形的每个内角都是120°,则n的值是()
| A.3 | B.4 | C.6 | D.8 |
如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:
①△DFE是等腰直角三角形;
②四边形CEDF不可能为正方形;
③四边形CEDF的面积随点E位置的改变而发生变化;
④点C到线段EF的最大距离为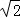 .
.
其中正确结论的个数是()
A、1个 B、2个 C、3个 D、4个
试题篮
()