初中数学圆内接四边形的性质选择题

如图，分别以直角△ABC的斜边AB，直角边AC为边向△ABC外作等边△ABD和等边△ACE，F为AB的中点，DE与AB交于点G，EF与AC交于点H，∠ACB=90°，∠BAC=30°．给出如下结论：
①EF⊥AC；②四边形ADFE为菱形；③AD=4AG；④FH=BD；其中正确结论的是（）

A．①②③

B．①②④

C．①③④

D．②③④

如图，在矩形ABCD中，BC=6，CD=3，将△BCD沿对角线BD翻折，点C落在点C¹处，BC¹交AD于点E，则线段DE的长为（）

A．3

B．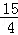

C．5

D．

如图，Rt△ABC中，∠C=90°，AC=3，BC=4．分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BDMC，四块阴影部分的面积分别为S₁、S₂、S₃、S₄．则S₁+S₂+S₃+S₄等于（）

A．14 B．16 C．18 D．20

如图，正方形 $\mathit{ABCD}$ 内接于 $\odot O$ ，线段 $\mathit{MN}$ 在对角线 $\mathit{BD}$ 上运动，若 $\odot O$ 的面积为 $2\pi$ ， $\mathit{MN}=1$ ，则 $\mathit{\Delta AMN}$ 周长的最小值是 $($ 　　 $)$

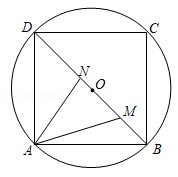
A．

3

B．

4

C．

5

D．

6

如图，在平面直角坐标系中，A(1,0)，B(0,3)，以AB为边在第一象限作正方形ABCD,点D在双曲线y=(k≠0)上，将正方形沿x轴负方向平移 m个单位长度后，点C恰好落在双曲线上，则m的值是（）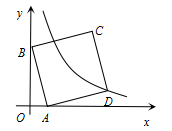

A．2

B．3

C．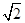

D．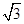

在平面直角坐标系中，正方形A₁B₁C₁D₁ 、D₁E₁E₂B₂、A₂B₂C₂D₂、D₂E₃E₄B₃、A₃B₃C₃D₃……按如图所示的方式放置，其中点B₁在y轴上，点C₁、E₁、E₂、C₂、E₃、E₄、C₃……在x轴上，已知正方形A₁B₁C₁D₁ 的边长为1，∠B₁C₁O=60°，B₁C₁∥B₂C₂∥B₃C₃……则正方形A₂₀₁₅B₂₀₁₅C₂₀₁₅D₂₀₁₅的边长是（）

A．

B．

C．

D．

如图1，在平面内选一定点O，引一条有方向的射线Ox，再选定一个单位长度，那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定，有序数对（θ，m）称为M点的“极坐标”，这样建立的坐标系称为“极坐标系”．在图2的极坐标系下，如果正六边形的边长为2，有一边OA在射线Ox上，则正六边形的顶点C的极坐标应记为（）

A．（60°，4）

B．（45°，4）

C．（60°，）

D．（50°，）

如图，ABCD是正方形场地，点E在DC的延长线上，AE与BC相交于点F．有甲、乙、丙三名同学同时从点A出发，甲沿着A﹣B﹣F﹣C的路径行走至C，乙沿着A﹣F﹣E﹣C﹣D的路径行走至D，丙沿着A﹣F﹣C﹣D的路径行走至D．若三名同学行走的速度都相同，则他们到达各自的目的地的先后顺序（由先至后）是（）

A．甲乙丙 B．甲丙乙 C．乙丙甲 D．丙甲乙

下列图形都是由同样大小的矩形按一定规律组成，其中第（1）个图形的面积为2，第（2）个图形的面积为8，第（3）个图形的面积为18，……，则第（10）个图形的面积为（）

A．196

B．200

C．216

D．256

如图，在平面直角坐标系中，菱形ABOC的顶点O在坐标原点，边BO在x轴的负半轴上，∠BOC=60°，顶点C的坐标为（m,3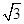），反比例函数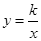的图像与菱形对角线AO交于D点，连接BD，当BD⊥x轴时，k的值是（）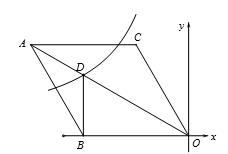

A．6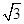

B．－6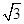

C．12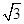

D．－12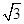

在 $\mathit{\Delta ABC}$ 中， $\angle \mathit{ACB}=90°$ ，分别过点 $B$ ， $C$ 作 $\angle \mathit{BAC}$ 平分线的垂线，垂足分别为点 $D$ ， $E$ ， $\mathit{BC}$ 的中点是 $M$ ，连接 $\mathit{CD}$ ， $\mathit{MD}$ ， $\mathit{ME}$ ．则下列结论错误的是 $($ 　　 $)$

A．

$\mathit{CD}=2\mathit{ME}$

B．

$\mathit{ME}//\mathit{AB}$

C．

$\mathit{BD}=\mathit{CD}$

D．

$\mathit{ME}=\mathit{MD}$

如图，在矩形ABCD中，AB＝3，BC＝4，点P在BC边上运动连结DP，过点A作AE⊥DP，垂足为E，设DP＝x，AE＝y，则能反映y与x之间函数关系的大致图象是（）

如图，周长为16的菱形ABCD中，点E，F分别在AB，AD边上，AE=1，AF=3，P为BD上一动点，则线段EP+FP的长最短为（）

A．3

B．4

C．5

D．6

如图，P为平行四边形ABCD内一点，过点P分别作AB、AD的平行线交平行四边形于E、F、G、H四点，若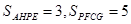，则为（）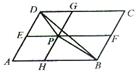

A．0．5 B．1 C．1．5 D．2

如图，已知正方形ABCD，点E是边AB的中点，点O是线段AE上的一个动点（不与A、E重合），以O为圆心，OB为半径的圆与边AD相交于点M，过点M作⊙O的切线交DC于点N，连接OM、ON、BM、BN．记△MNO、△AOM、△DMN的面积分别为S₁、S₂、S₃，则下列结论不一定成立的是（）

A．S₁＞S₂+S₃ B．△AOM∽△DMN C．∠MBN=45° D．MN=AM+CN