如图,在正方形ABCD中,AB=5,P是BC边上任意一点,E是BC延长
线上一点,连接AP,作PF⊥AP,使PF=PA,连接CF,AF,AF交CD边于点G,连接PG.
(1)求证:∠GCF=∠FCE;
(2)判断线段PG,PB与DG之间的数量关系,并证明你的结论;
(3)若BP=2,在直线AB上是否存在一点M,使四边形DMPF是平行四边形,若存在,求出BM的长度,若不存在,说明理由.
已知四边形ABCD中AD//BC,AD:BC=1:2,SDAOF:SDDOE=1:3,SDBEF="24" cm2,求rAOF的面积。
如图,Rt△ 中,
中, ,
, ,
,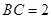 ,
,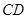 是斜边
是斜边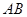 上的高,点
上的高,点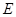 为边
为边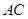 上一点(点
上一点(点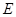 不与点
不与点 、
、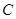 重合),连接
重合),连接 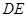 ,作
,作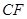 ⊥
⊥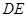 ,
,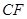 与边
与边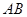 、线段
、线段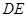 分别交于点
分别交于点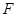 ,
, ;
;
(1)求线段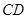 、
、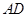 的长;
的长;
(2)设 ,
,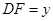 ,求
,求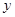 关于
关于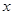 的函数解析式,并写出x的取值范围.
的函数解析式,并写出x的取值范围.
(25分)已知G是△ABC内任一点,BG、CG分别交AC、AB于点E、F.
求使不等式S△BGF·S△CGE≤kS2△ABC恒成立的k的最小值.
如图1,在矩形纸片ABCD中, ,其中m≥1,将该矩形沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,MN与CD相交于点P,连接EP.设
,其中m≥1,将该矩形沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,MN与CD相交于点P,连接EP.设 ,其中0<n≤1.
,其中0<n≤1.
(1)如图2,当 (即M点与D点重合),
(即M点与D点重合), 时,则
时,则 ;
;
(2)如图3,当 (M为AD的中点),m的值发生变化时,求证:
(M为AD的中点),m的值发生变化时,求证: ;
;
(3)如图1,当 ,n的值发生变化时,
,n的值发生变化时, 的值是否发生变化?说明理由.
的值是否发生变化?说明理由.
如图,矩形ABCD的边AB=3cm,AD=4cm,点E从点A出发,沿射线AD移动,以CE为直径作圆O,点F为圆O与射线BD的公共点,连接EF、CF,过点E作EG⊥EF,EG与圆O相交于点G,连接CG.
(1)试说明四边形EFCG是矩形;
(2)当圆O与射线BD相切时,点E停止移动,在点E移动的过程中,
①矩形EFCG的面积是否存在最大值或最小值?若存在,求出这个最大值或最小值;若不存在,说明理由;
②求点G移动路线的长.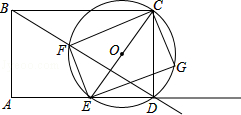
设a、b、c和S分别为三角形的三边长和面积,关于x的方程b2x2+(b2+c2-a2)x+c2=0的判别式为Δ.则Δ与S的大小关系为( ).
| A.Δ=16S2 | B.Δ=-16S2 | C.Δ=16S | D.Δ=-16S |
在Rt△ABC中,∠ACB=90°,AC=BC,D为AB边的中点,点P为BC边上一点,把△PBD沿PD翻拆,点B落在点E处,设PE交AC于F,连接CD
(1)求证:△PCF的周长= CD;
CD;
(2)设DE交AC于G,若 ,CD=6,求FG的长
,CD=6,求FG的长
已知△ABC,以AC为边在△ABC外作等腰△ACD,其中AC=AD.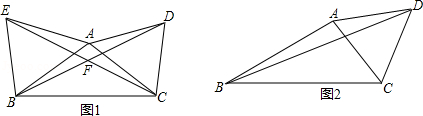
(1)如图1,若AB=AE,∠DAC=∠EAB=60°,求∠BFC的度数;
(2)如图2,∠ABC=α,∠ACD=β,BC=4,BD=6.
①若α=30°,β=60°,AB的长为;
②若改变α,β的大小,但α+β=90°,△ABC的面积是否变化?若不变,求出其值;若变化,说明变化的规律.
(本题12分)如图,ABCD是一张矩形纸片,AD=BC=1,AB=CD=5.在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK.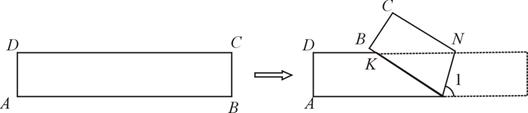
(1)若∠1=70°,求∠MKN的度数.
(2)△MNK的面积能否小于 ?若能,求出此时∠1的度数;若不能,试说明理由.
?若能,求出此时∠1的度数;若不能,试说明理由.
(3)如何折叠能够使△MNK的面积最大?请你利用备用图探究可能出现的情况,求出最大值.
如图,在矩形ABCD中,AB=20cm,BC=4cm,点p从A开始折线A——B——C——D以4cm/秒的 速度 移动,点Q从C开始沿CD边以1cm/秒的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达D时,另一点也随之停止运动,设运动的时间t(秒)
(1)t为何值时,四边形APQD为矩形.
(2)如图(2),如果⊙P和⊙Q的半径都是2cm,那么t为何值时,⊙P和⊙Q外切?
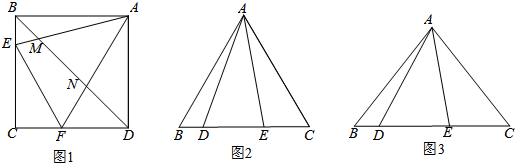
(1)如图1,点E、F分别是正方形ABCD的边BC、CD上的点,∠EAF=45°,连接EF,
则EF、BE、FD之间的数量关系是:EF=BE+FD.连结BD,交AE、AF于点M、N,且MN、BM、DN满足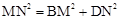 ,请证明这个等量关系;
,请证明这个等量关系;
(2)在△ABC中, AB=AC,点D、E分别为BC边上的两点.
①如图2,当∠BAC=60°,∠DAE=30°时,BD、DE、EC应满足的等量关系是__________________;
②如图3,当∠BAC= ,(0°<
,(0°< <90°),∠DAE=
<90°),∠DAE= 时,BD、DE、EC应满足的等量关系是____________________.【参考:
时,BD、DE、EC应满足的等量关系是____________________.【参考: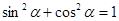 】
】
试题篮
()