在下列四组线段中,能组成直角三角形的是()
| A.4,5,6 | B.5,6,10 |
C. , , , , |
D.5,8,12 |
如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC≌△AED的条件有()
| A.4个 | B.3个 | C.2个 | D.1个 |
如图,△ABC和△DEF中,AB=DE、∠B=∠DEF,添加下列哪一个条件无法证明△ABC≌△DEF()
| A.AC∥DF | B.∠A=∠D | C.AC="DF" | D.∠ACB=∠F |
在△ABC和△A′B′C′中,AB=A′B′,∠B=∠B′,补充条件后,仍不一定能保证△ABC≌△A′B′C′,这个补充条件是()
| A.BC=B′C′ | B.∠A=∠A′ |
| C.AC=A′C′ | D.∠C=∠C′ |
如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是()
| A.三角形的稳定性 | B.两点之间线段最短 |
| C.两点确定一条直线 | D.垂线段最短 |
在下列长度的各组线段中,能构成直角三角形的是()
| A.3,5,9 | B.4,6,8 |
C.1,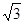 ,2 ,2 |
D.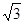 , ,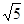 , ,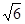 |
如图,在直角三角形ABC中,∠B=90°,以下式子成立的是()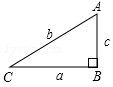
| A.a2+b2=c2 | B.a2+c2=b2 | C.b2+c2=a2 | D.(a+c)2=b2 |
在下列长度的四根木棒中,能与两根长度分别为4cm和9cm的木棒构成一个三角形的是()
| A.4cm | B.5cm | C.9cm | D.13cm |
如图,在△ABC中,∠A=80°,∠B=40°.D、E分别是AB,AC上的点,且DE∥BC,则∠AED的度数是()
A.40° B.60° C.80° D.120°
如果三角形的两边长分别为3和5,第三边长是偶数,则第三边长可以是()
| A.2 | B.3 | C.4 | D.8 |
两根木棒的长度分别是5cm和7cm,要选择第三根木棒,将它们钉成一个三角形,如果第三根木棒的长为偶数,那么第三根木棒长的取值情况有()
| A.3种 | B.4种 | C.5种 | D.6种 |
如图,下面是利用尺规作∠AOB的角平分线OC的作法,在用尺规作角平分线时,用到的三角形全等的判定方法是()
作法:以O为圆心,任意长为半径作弧,交OA,OB于点D, E.分别以D,E为圆心,以大于 DE的长为半径作弧,两弧在∠AOB内交于点C.作射线OC.则OC就是∠AOB的平分线.
DE的长为半径作弧,两弧在∠AOB内交于点C.作射线OC.则OC就是∠AOB的平分线.
A.SSS B.SAS C.ASA D.AAS
试题篮
()