(本小题满分18分)某校八(1)班同学为了解2011年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,
月均用水量 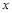 (t) (t) |
频数(户) |
频率 |
 |
6 |
0.12 |
 |
0.24 |
|
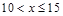 |
16 |
0.32 |
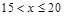 |
10 |
0.20 |
 |
4 |
|
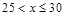 |
2 |
0.04 |
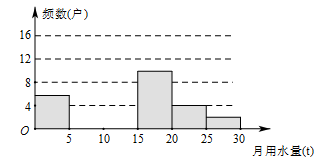
请解答以下问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)若该小区用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20 t的家庭大约有多少户?
(本小题满分10分)已知:如图,  ,
,  是□ABCD的对角线
是□ABCD的对角线 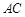 上的两点,
上的两点,  ,求证:
,求证:  .
. 
股民王海上星期六买进某公司的股票3000股,每股17元,下表为本周内每日股票的涨跌情况(单位:元)
| 星期 |
一 |
二 |
三 |
四 |
五 |
六 |
| 每股涨跌 |
+4 |
+4.5 |
-1 |
-2.5 |
-6 |
+2 |
试问:
(1)本周内,每股的最高价是多少元?最低价是多少元?分别是星期几?
(2)以上星期六为0点,画出本周内股票价格涨跌情况的折线图.
出租车司机小李某天下午运营全是在东西走向的人民大道上进行的,如果规定向东为正,向西为负,这天下午他的行车里程(单位:千米)如下:
+15,-2,+5,-1,+10,-3,-2,+12,+4,-5,+6
(1)将最后一名乘客送到目的地时,小李距下午出车时的出发点多远?
(2)若汽车耗油量为3升/千米,这天下午小李共耗油多少升?
假如圆锥的体积一定,它的底面直径与高()
| A.成正比例 | B.成反比例 | C.不成比例 | D.无法确定 |
(本题6分)如图1是用硬纸板做成的两个全等的直角三角形,两直角边的长分别为a和b,斜边长为c,如图2是以c为直角边的等腰直角三角形.请你开动脑筋,将它们拼成一个能证明勾股定理的图形.
(1)画出拼成的这个图形的示意图;
(2)用这个图形证明勾股定理;
(3)假设图1中的直角三角形有若干个,你能只运用图1中所给的直角三角形拼出另一种能证明勾股定理的图形吗?请画出拼后的示意图(无需证明).
(本题5分)如图是某市的部分简图,如果少年宫的坐标为(-3, 1),宾馆的坐标为(2, 2),请建立适当的平面直角坐标系,并分别写出其余四个地方的坐标.
如图,在△ACB中,∠ACB=90°,CD⊥AB于D.
(1)求证:∠ACD=∠B;
(2)若AF平分∠CAB分别交CD、BC于E、F,求证:∠CEF=∠CFE.
试题篮
()