如图,射线 和射线 相交于点 , ,且 .点 是射线 上的动点(点 不与点 和点 重合),作射线 ,并在射线 上取一点 ,使 ,连接 , .
(1)如图①,当点 在线段 上, 时,请直接写出 的度数;
(2)如图②,当点 在线段 上, 时,请写出线段 , , 之间的数量关系,并说明理由;
(3)当 , 时,请直接写出 的值.

如图1, 中,点 , , 分别在边 , , 上, ,点 在线段 上, , , .

(1)填空:与 相等的角是 ;
(2)用等式表示线段 与 的数量关系,并证明;
(3)若 , (如图 ,求 的值.
如图, 是 的直径,点 ,点 在 上, , 与 相交于点 , 与 相切于点 ,与 延长线相交于点 .
(1)求证: .
(2)若 , ,求 的半径.

如图,在菱形 中, ,点 , 分别在 , 上,且 , 与 相交于点 , 与 相交于点 .下列结论:① ;② ;③若 ,则 ;④ .其中正确的结论有 .(只填序号即可)

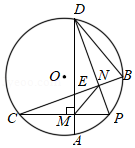
如图,在 中,点 为 的中点,弦 、 互相垂直,垂足为 , 分别与 、 相交于点 、 ,连接 、 .
(1)求证: 为 的中点.
(2)若 的半径为8, 的度数为 ,求线段 的长.
初步尝试
(1)如图①,在三角形纸片 中, ,将 折叠,使点 与点 重合,折痕为 ,则 与 的数量关系为 ;
思考说理
(2)如图②,在三角形纸片 中, , ,将 折叠,使点 与点 重合,折痕为 ,求 的值;
拓展延伸
(3)如图③,在三角形纸片 中, , , ,将 沿过顶点 的直线折叠,使点 落在边 上的点 处,折痕为 .
①求线段 的长;
②若点 是边 的中点,点 为线段 上的一个动点,将 沿 折叠得到△ ,点 的对应点为点 , 与 交于点 ,求 的取值范围.

如图,在 中, , 平分 交 于点 ,过点 和点 的圆,圆心 在线段 上, 交 于点 ,交 于点 .
(1)判断 与 的位置关系,并说明理由;
(2)若 , ,求 的长.
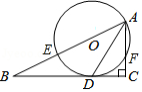
如图,在 中, ,点 在 上,以 为半径的半圆 交 于点 ,交 于点 ,过点 作半圆 的切线 ,交 于点 .
(1)求证: ;
(2)若 , , ,求半圆 的半径长.

如图,在 中, ,以斜边 上的中线 为直径作 ,与 交于点 ,与 的另一个交点为 ,过 作 ,垂足为 .
(1)求证: 是 的切线;
(2)若 的直径为5, ,求 的长.

匈牙利著名数学家爱尔特希
.
,
曾提出:在平面内有
个点,其中每三个点都能构成等腰三角形,人们将具有这样性质的
个点构成的点集称为爱尔特希点集.如图,是由五个点
、
、
、
、
构成的爱尔特希点集(它们为正五边形的任意四个顶点及正五边形的中心构成),则
的度数是 .
如图1, 是 的直径,直线 与 相切于点 ,直线 与 相切于点 ,点 (异于点 在 上,点 在 上,且 ,延长 与 相交于点 ,连接 并延长交 于点 .

(1)求证: 是 的切线;
(2)求证: ;
(3)如图2,连接 并延长与 分别相交于点 、 ,连接 .若 , ,求 .
如图, 为 的直径,四边形 内接于 ,对角线 , 交于点 , 的切线 交 的延长线于点 ,切点为 ,且 .
(1)求证: ;
(2)若 , ,求 的值.

如图,在 中, 为斜边 的中线,过点 作 于点 ,延长 至点 ,使 ,连接 , ,点 在线段 上,连接 ,且 , , .下列结论:
① ;
②四边形 是平行四边形;
③ ;
④ .
其中正确结论的个数是

| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |
试题篮
()