如图1,在正方形 中, 平分 ,交 于点 ,过点 作 ,交 的延长线于点 ,交 的延长线于点 .
(1)求证: ;
(2)如图2,连接 、 ,求证: 平分 ;
(3)如图3,连接
交
于点
,求
的值.
如图,点 是以 为直径的 上一点,过点 作 的切线,交 的延长线于点 , 是 的中点,连接 并延长与 的延长线交于点 .
(1)求证: 是 的切线;
(2)若 , ,求 的长.
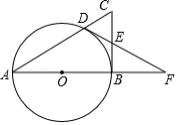
如图1,在 中, , ,点 为 边上的动点(点 不与点 , 重合).以 为顶点作 ,射线 交 边于点 ,过点 作 交射线 于点 ,连接 .
(1)求证: ;
(2)当 时(如图 ,求 的长;
(3)点 在 边上运动的过程中,是否存在某个位置,使得 ?若存在,求出此时 的长;若不存在,请说明理由.
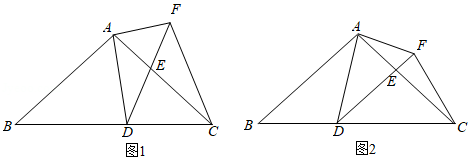
在 中, 平分 交 于点 .

(1)如图1,若 , ,求 的面积;
(2)如图2,过点 作 ,交 的延长线于点 ,分别交 , 于点 , ,且 .求证: .
如图,在 中, , 是 边上的中点,连结 , 平分 交 于点 ,过点 作 交 于点 .
(1)若 ,求 的度数;
(2)求证: .

如图, 已知: 是 的弦, 过点 作 交 于点 ,过点 作 的切线交 的延长线于点 ,取 的中点 ,过点 作 交 的延长线于点 ,连接 并延长交 的延长线于点 .
求证:
(1) ;
(2) .
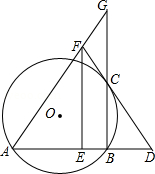
如图,在 中, , , ,动点 从点 出发,沿 以每秒2个单位长度的速度向终点 运动.过点 作 于点 (点 不与点 、 重合),作 ,边 交射线 于点 .设点 的运动时间为 秒.
(1)用含 的代数式表示线段 的长;
(2)当点 与点 重合时,求 的值;
(3)设 与 重叠部分图形的面积为 ,求 与 之间的函数关系式;
(4)当线段 的垂直平分线经过 一边中点时,直接写出 的值.

在等边 中,

(1)如图1, , 是 边上的两点, , ,求 的度数;
(2)点 , 是 边上的两个动点(不与点 , 重合),点 在点 的左侧,且 ,点 关于直线 的对称点为 ,连接 , .
①依题意将图2补全;
②小茹通过观察、实验提出猜想:在点 , 运动的过程中,始终有 ,小茹把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证明 ,只需证 是等边三角形;
想法2:在 上取一点 ,使得 ,要证明 ,只需证 ;
想法3:将线段 绕点 顺时针旋转 ,得到线段 ,要证 ,只需证 ,
请你参考上面的想法,帮助小茹证明 (一种方法即可).
(年贵州省遵义市)如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交CA的延长线于点E,连接AD、DE.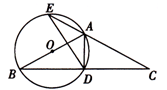
(1)求证:D是BC的中点;
(2)若DE=3,BD—AD=2,求⊙O的半径;
(3)在(2)的条件下,求弦AE的长.
试题篮
()