如图1,在等腰梯形ABCD中,∠B=60°,P、Q同时从B出发,以每秒1单位长度分别沿B-A-D-C和B-C-D方向运动至相遇时停止,设运动时间为t(秒),△BPQ的面积为S(平房单位),S与t的函数图象如图2所示,则下列结论错误的是()
A.当t=4秒时,S=4 |
| B.AD=4 |
C.当4≤t≤8时,S=2 t t |
| D.当t=9秒时,BP平分梯形ABCD的面积 |
如图,正方形ABCD的面积为4,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
| A.2 | B.3 | C.2 |
D. |
如图,ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,∠DCE=30°,若OE=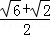 ,则正方形的面积为( )
,则正方形的面积为( )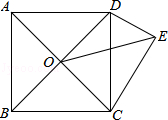
A.5 B.4 C.3 D.2
在面积为15的平行四边形ABCD中,过点A作AE垂直于直线BC于点E,作AF垂直于直线CD于点F,若AB=5,BC=6,则CE+CF的值为( )
A.11+ |
B.11﹣ |
C.11+ 或11﹣ 或11﹣ |
D.11+ 或1+ 或1+ |
如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是( )
A. |
B. |
C. |
D. |
在矩形ABCD中,已知AB=2cm,BC=3cm,现有一根长为2 cm的木棒EF紧贴着矩形的边(即两个端点始终落在矩形的边上),按逆时针方向滑动一周,则木棒EF的中点P在运动过程中所围成的图形的面积为()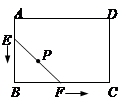
| A.6 cm2 | B.3 cm2 | C.(2+π)cm2 | D.(6-π)cm2 |
如图1,菱形ABCD的对角线交于点O,AC=2BD,点P是AO上一个动点,过点P作AC的垂线交菱形的边于M,N两点.设AP=x,△OMN的面积为y, 表示y与x的函数关系的图象大致如图2所示,则菱形的周长为()
| A.2 | B. |
C.4 | D.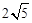 |
如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为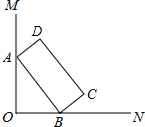
A.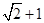 B.
B.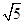 C.
C.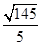 D.
D.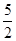
如图,在矩形 中,点A的坐标是(-2,1),点C的纵坐标是4,则B、C两点的坐标为()
中,点A的坐标是(-2,1),点C的纵坐标是4,则B、C两点的坐标为()
A.( ,
, )、(
)、( ,
, )B.(
)B.( ,
, )、(
)、( ,
, )
)
C.( ,
, )、(
)、( ,
, )D.(
)D.( ,
, ) 、(
) 、( ,
, )
)
如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )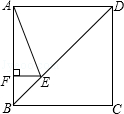
| A.1 | B.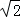 |
C.4﹣2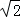 |
D.3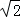 ﹣4 ﹣4 |
如图,在斜边为3的等腰直角三角形OAB中,作内接正方形A1B1C1D1;在等腰直角三角形OA1B1中,作内接正方形A2B2C2D2;在等腰直角三角形OA2B2中,作内接正方形A3B3C3D3…依次作下去,则第2014个正方形A2014B2014C2014D2014的边长是( )
A. |
B. |
C. |
D. |
如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )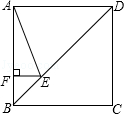
| A.1 | B.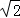 |
C.4﹣2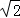 |
D.3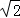 ﹣4 ﹣4 |
正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,正方形BEFG的边长为4,则△DEK的面积为( )
A.10B.12C.14D.16
试题篮
()