如图,在Rt△ABC中,∠BAC=90°,D、E分别是AB、BC的中点,F在CA的延长线上,∠FDA=∠B,AC=6,AB=8,则四边形AEDF的周长为()
A.22 B.20 C.18 D.16
如图,点D是△ABC的边AB的延长线上一点,点F是边BC上的一个动点(不与点B重合),以BD、BF为邻边作平行四边形BDEF,又AP綊BE(点P、E在直线AB的同侧),如果BD= AB,那么△PBC的面积与△ABC的面积之比为( )
AB,那么△PBC的面积与△ABC的面积之比为( )
A. B.
B. C.
C. D.
D.
如图,两个边长相等的正方形ABCD和EFGH,正方形EFGH的顶点E固定在正方形ABCD的对称中心位置,正方形EFGH绕点E顺时针方向旋转,设它们重叠部分的面积为S,旋转的角度为θ,S与θ的函数关系的大致图象是( )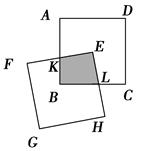
如图,边长为1的菱形ABCD绕点A旋转,当B、C两点恰好落在扇形AEF的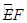 上时,
上时,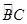 的长度等于( ).
的长度等于( ).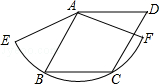
A.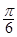 B.
B.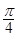 C.
C.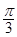 D.
D.
在矩形ABCD中,AB=1,AD= ,AF平分∠DAB,过C点作CE
,AF平分∠DAB,过C点作CE BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②B0=BF;③CA=CH;④BE=3ED;正确的个数为( )
BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②B0=BF;③CA=CH;④BE=3ED;正确的个数为( )
| A.1个 | B.2个 | C.3个 | D.4个 |
如图,正方形ABCD的边长为4,P为正方形边上一动点,沿A→D→C→B→A 的路径匀速移动,设P点经过的路径长为x,△APD的面积是y,则下列图象能大致反映y与x的函数关系的是
A. |
B. |
C. |
D. |
设边长为3的正方形的对角线长为a,下列关于a的四种说法:① a是无理数;② a可以用数轴上的一个点来表示;③ 3<a<4;④ a是18的算术平方根。其中,所有正确说法的序号是
| A.①④ | B.②③ | C.①②④ | D.①③④ |
在直线l上依次摆放着七个正方形(如图所示)。已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4,则S1+S2+S3+S4的值为( )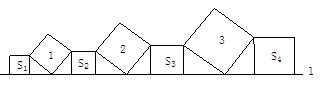
| A.6 | B.5 | C.4 | D.3 |
如图,在平面直角坐标系中,四边形OABC是菱形,点C的坐标为(4,0)∠AOC= 60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形OABC的两边分别交于点M,N(点M在点N的上方),若△OMN的面积为S,直线l的运动时间为t 秒(0≤t≤4),则能大致反映S与t的函数关系的图象是( ) 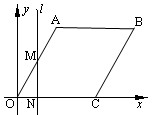
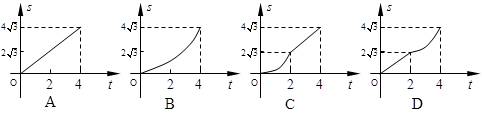
如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为 cm的正方形
cm的正方形 ,剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的面积()
,剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的面积()
A. |
B. |
C. |
D. |
试题篮
()