初中数学选择题

不等式组的解集是（）

A．

B．

C．

D．

在平面直角坐标系中，四边形OABC是矩形，点B的坐标为（4，3）．平行于对角线AC的直线m从原点O出发，沿x轴正方向以每秒1个单位长度的速度运动，设直线m与矩形OABC的两边分别交于点M，N，直线m运动的时间为t（秒）．设△OMN的面积为S，那么能反映S与t之间函数关系的大致图象是（）

A．

B．

C．

D．

如图，在半径为6cm的⊙O中， A点是劣弧的中点，点D是优弧上一点，且∠D=30°，下列四个结论：

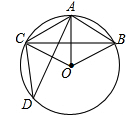
①OA⊥BC；②BC=6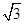m；③sin∠AOB=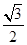；④四边形ABOC是菱形．
其中正确结论的序号是（）

A．①③

B．①②③④

C．②③④

D．①③④

如图，已知在Rt△ABC中，AB=AC=2，在△ABC内作第一个内接正方形DEFG；然后取GF的中点P，连接PD、PE，在△PDE内作第二个内接正方形HIKJ；再取线段KJ的中点Q，在△QHI内作第三个内接正方形…依次进行下去，则第n个内接正方形的边长为（）

A、 B、 C、 D、

设二次函数y₁=a（x−x₁）（x−x₂）（a≠0，x₁≠x₂）的图象与一次函数y₂=dx+e（d≠0）的图象交于点（x₁，0），若函数y=y₂+y₁的图象与x轴仅有一个交点，则（）

A．a（x1−x2）=d	B．a（x2−x1）="d"
C．a（x1−x2）^2=d	D．a（x1+x2）^2=d

某企业为了解员工给灾区“爱心捐款”的情况，随机抽取部分员工的捐款金额整理绘制成如图所示的直方图，根据图中信息，下列结论正确的是（）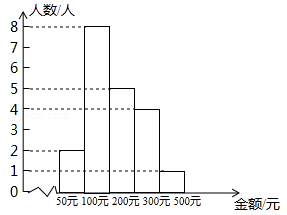

A．样本中位数是200元

B．样本容量是20

C．该企业员工捐款金额的极差是450元

D．该企业员工最大捐款金额是500元

设a为的小数部分，b为的小数部分.则的值为（）.

A．+-1	B．-+1
C．--1	D．++1

如图，AB=10，C是线段AB上一点，分别以AC、CB为边在AB的同侧作等边△ACP和等边△CBQ，连结PQ，则PQ的最小值是（）

A．5B．6C．3D．4

如图，矩形AOBC中，顶点C的坐标（4，2），又反比例函数y＝的图像经过矩形的对角线的交点P，则该反比例函数关系式是（）

A．y＝（x＞0）	B．y＝（x＞0）
C．y＝（x＞0）	D．y＝（x＞0）

如图，在▱ABCD中，BC=2AB，点M是AD的中点，CF⊥AB于F，如果∠AFM=50°，则∠B的度数为（）

A．80°

B．100°

C．50°

D．40°

如图，两个边长相等的正方形ABCD和EFGH，正方形EFGH的顶点E固定在正方形ABCD的对称中心位置，正方形EFGH绕点E顺时针方向旋转，设它们重叠部分的面积为S，旋转的角度为θ，S与θ的函数关系的大致图象是（）

如图，点D是△ABC的边AB的延长线上一点，点F是边BC上的一个动点（不与点B重合），以BD、BF为邻边作平行四边形BDEF，又AP∥BE，且AP="BE" （点P、E在直线AB的同侧），如果BD＝AB，那么△PBC的面积与△ABC的面积之比为（）

A． B． C． D．

若三角形ΔABC的周长为20cm，点D,E,F分别是三边的中点，则DEF的周长为（）

A．5cm

B．10cm

C．15cm

D．6cm

如图，在Rt∠AOB的平分线ON上依次取点C，F，M，过点C作DE⊥OC，分别交OA，OB于点D，E，以FM为对角线作菱形FGMH，已知∠DFE=∠GFH=120°，FG=FE。设OC=x，图中阴影部分面积为y，则y与x之间的函数关系式是（）

A．

B．

C．

D．

如图，在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG，动点P从点A出发，沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止（不含点A和点B），则△ABP的面积S随着时间t变化的函数图像大致为（）