如图,下列各图形中的三个数之间均具有相同的规律.根据此规律,图形中M与m、n的关系是()
| A.M=mn | B.M=m(n+1) | C.M=mn+1 | D.M=n(m+1) |
如图,△ABC中,∠ACB=90°,∠A=30°,AB=16.点P是斜边AB上一点.过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q,设AP=x,△APQ的面积为y,则y与x之间的函数图象大致为()
如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为()
| A.(60°,4) | B.(45°,4) | C.(60°, ) ) |
D.(50°, ) ) |
某种细菌在培养过程中,每半个小时分裂一次(由1个分裂成2个,两个裂成4个…),若这种细菌由1个分裂成128个,那么这个过程需要经过()小时。
A. |
B.3 | C. |
D. |
如图,已知抛物线 和直线
和直线 .我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M= y1=y2.
.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M= y1=y2.
下列判断:
①当x>2时,M=y2;
②当x<0时,x值越大,M值越大;
③使得M大于4的x值不存在;
④若M=2,则x=" 1" .其中正确的有()
| A.1个 | B.2个 | C.3个 | D.4个 |
如图,在平面直角坐标系中,抛物线 经过平移得到抛物线
经过平移得到抛物线 ,其对称轴与两段抛物线所围成的阴影部分的面积是()
,其对称轴与两段抛物线所围成的阴影部分的面积是()
| A.2 | B.4 | C.8 | D.16 |
如图,△ABC中,AB=4,AC=3,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为()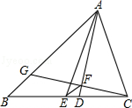
A.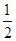 B.1 C.
B.1 C.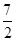 D.7
D.7
如图,E是边长为l的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R,则PQ+PR的值为() 
A. |
B. |
C. |
D. |
如图反映的过程是:矩形 中,动点
中,动点 从点
从点 出发,依次沿对角线
出发,依次沿对角线 、边
、边 、边
、边 运动至点
运动至点 停止,设点
停止,设点 的运动路程为
的运动路程为 ,
,  .则矩形
.则矩形 的周长是
的周长是

| A.6 | B.12 | C.14 | D.15 |
如图,点A、B、C、D为圆O的四等分点,动点P从圆心O出发,沿线段OC- -线段DO的路线作匀速运动.设运动时间为
-线段DO的路线作匀速运动.设运动时间为 秒,∠APB的度数为y度,则下列图象中表示y与t的函数关系最恰当的是 ()
秒,∠APB的度数为y度,则下列图象中表示y与t的函数关系最恰当的是 ()

如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的 后得到线段CD,则端点C的坐标为( )
后得到线段CD,则端点C的坐标为( )
| A.(3,3) | B.(4,3) | C.(3,1) | D.(4,1) |
如图,A,B两地被池塘隔开,小明通过下列方法测出了A,B间的距离:先在AB外选一点C,然后找出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A,B间的距离.有关他这次探究活动的描述错误的是( )
| A.AB=24m | B.MN∥AB |
| C.△CMN∽△CAB | D.CM︰MA=1︰2 |
如图,在△ABC中,D,E分别是AB,BC上的点,且DE∥AC.若S△BDE︰S△CDE=1︰4,则S△BDE︰S△ACD=( )
A.1︰16 B.1︰18
C.1︰20 D.1︰24
试题篮
()