如图1,正方形纸片ABCD的边长为2,翻折∠B、∠D,使得两个直角的顶点重合于对角线BD上一点P,EF、GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断:
①当x=1时,点P是正方形ABCD的中心;
②当x= 时,EF+GH>AC;
时,EF+GH>AC;
③当0<x<2时,六边形AEFCHG面积的最大值是 ;
;
④当0<x<2时,六边形AEFCHG周长的值不变.
其中正确的是________(填序号).
已知△ABC内接于⊙O,过点A作直线EF.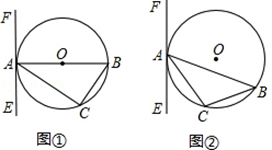
(1)如图①所示,若AB为⊙O的直径,要使EF成为⊙O的切线,还需要添加的一个条件是(至少说出两种): 或者 .
(2)如图②所示,如果AB是不过圆心O的弦,且∠CAE=∠B,那么EF是⊙O的切线吗?试证明你的判断.
如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从4这点开始跳,则经2015次跳后它停在数 对应的点上.
已知正比例函数y1=x,反比例函数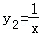 ,由y1,y2构造一个新函数y=x+
,由y1,y2构造一个新函数y=x+ 其图象如图所示.(因其图象似双钩,我们称之为“双钩函数”).给出下列几个命题:
其图象如图所示.(因其图象似双钩,我们称之为“双钩函数”).给出下列几个命题: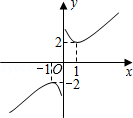
①该函数的图象是中心对称图形;
②当x<0时,该函数在x=﹣1时取得最大值﹣2;
③y的值不可能为1;
④在每个象限内,函数值y随自变量x的增大而增大.
其中正确的命题是 .(请写出所有正确的命题的序号)
用黑白两种颜色正方形的纸片按黑色纸片数逐渐加l的规律拼成一列图案:第n个图案中有白色纸片___________张.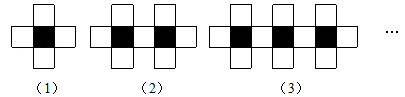
已知:如图,有长为24米的篱笆,一面利用墙(墙的最大可用长度a为10米),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x米,面积为S米2.则S与x的函数关系式 ;自变量的取值范围 .
数学家发明了一个魔术盒,当任意数对(a,b)放入其中时,会得到一个新的数:a2+b+1.例如把(3,﹣2)放入其中,就会得到32+(﹣2)+1=8.现将数对(﹣2,3)放入其中得到数m= ,再将数对(m,1)放入其中后,得到的数是 .
如图,在 中, , , ,点 在边 上, ,联结 .如果将 沿直线 翻折后,点 的对应点为点 ,那么点 到直线 的距离为 .

如图,一段抛物线:y=﹣x(x﹣3)(0≤x≤3),记为C1,它与x轴交于点O,A1;
将C1绕点A1旋转180°得C2,交x轴于点A2;
将C2绕点A2旋转180°得C3,交x轴于点A3;
…
如此进行下去,直至得C2015.
若P(m,2),在第2015段抛物线C2015上,则m= 6043或6044 .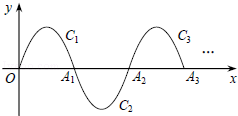
如图,抛物线 与 轴交于点 ,点 ,与 轴交于点 ,且过点 .点 、 是抛物线 上的动点.
(1)求抛物线的解析式;
(2)当点 在直线 下方时,求 面积的最大值.
(3)直线 与线段 相交于点 ,当 与 相似时,求点 的坐标.

某企业有 , 两条加工相同原材料的生产线.在一天内, 生产线共加工 吨原材料,加工时间为 小时;在一天内, 生产线共加工 吨原材料,加工时间为 小时.第一天,该企业将5吨原材料分配到 , 两条生产线,两条生产线都在一天内完成了加工,且加工时间相同,则分配到 生产线的吨数与分配到 生产线的吨数的比为 .第二天开工前,该企业按第一天的分配结果分配了5吨原材料后,又给 生产线分配了 吨原材料,给 生产线分配了 吨原材料.若两条生产线都能在一天内加工完各自分配到的所有原材料,且加工时间相同,则 的值为 .
试题篮
()