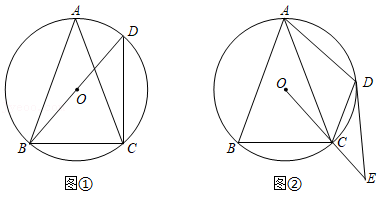
已知 内接于 , , ,点 是 上一点.
(Ⅰ)如图①,若 为 的直径,连接 ,求 和 的大小;
(Ⅱ)如图②,若 ,连接 ,过点作 的切线,与 的延长线交于点 ,求 的大小.
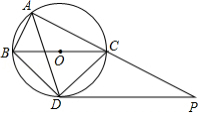
如图, 是 的外接圆,点 在 边上, 的平分线交 于点 ,连接 , ,过点 作 的切线与 的延长线交于点 .
(1)求证: ;
(2)求证: ;
(3)当 , 时,求线段 的长.
如图, 内接于 , 平分 交 边于点 ,交 于点 ,过点 作 于点 ,设 的半径为 , .
(1)过点 作直线 ,求证: 是 的切线;
(2)求证: ;
(3)设 ,求 的值(用含 的代数式表示).

如图, 内接于 , 为 的直径, , ,连结 ,弦 分别交 , 于点 , ,其中点 是 的中点.
(1)求证: .
(2)求 的长.

如图,已知 是 的内接三角形, 是 的直径,连结 , 平分 .
(1)求证: ;
(2)若 ,求 的长.
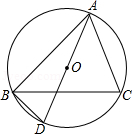
如图,在 中, .
(1)尺规作图:作 的外接圆 ;作 的角平分线交 于点 ,连接 .(不写作法,保留作图痕迹)
(2)若 , ,求 的长.

如图, 是 的 边上一点,连接 ,作 的外接圆,将 沿直线 折叠,点 的对应点 落在 上.
(1)求证: .
(2)若 , , ,求 的长.

如图,已知等腰直角三角形 ,点 是斜边 上一点(不与 , 重合), 是 的外接圆 的直径.
(1)求证: 是等腰直角三角形;
(2)若 的直径为2,求 的值.

如图,在直角三角形 中, ,点 是 的内心,
的延长线和三角形 的外接圆 相交于点 ,连接 .
(1)求证: ;
(2)过点 作 的平行线交 、 的延长线分别于点 、 ,已知 ,圆 的直径为5.
①求证: 为圆 的切线;
②求 的长.

阅读下列材料:
已知:如图1,等边△ 内接于 ,点 是 上的任意一点,连接 , , ,可证: ,从而得到: 是定值.

(1)以下是小红的一种证明方法,请在方框内将证明过程补充完整;
证明:如图1,作 , 交 的延长线于点 .
△ 是等边三角形,
,
又 , ,
△ △

.
,是定值.
(2)延伸:如图2,把(1)中条件“等边△ ”改为“正方形 ”,其余条件不变,请问: 还是定值吗?为什么?
(3)拓展:如图3,把(1)中条件“等边△ ”改为“正五边形 ”,其余条件不变,则 (只写出结果).
如图,以 为直径的 外接于 ,过 点的切线 与 的延长线交于点 , 的平分线分别交 , 于点 , ,其中 , 的长是一元二次方程 的两个实数根.
(1)求证: ;
(2)在线段 上是否存在一点 ,使得四边形 是菱形?若存在,请给予证明,并求其面积;若不存在,说明理由.
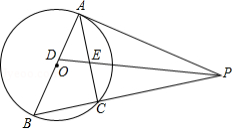
如图, 是 的外接圆, 为直径,点 为 外一点,且 ,连接 交 于点 ,延长 交 于点 .
(1)证明: ;
(2)若 ,证明: 是 的切线;
(3)在(2)条件下,连接 交 于点 ,连接 ,若 ,求 的长.

如图, 内接于 ,点 在 外, , 交 于点 ,交 于点 , , , , .
(1)求证: ;
(2)求证:
是
的切线;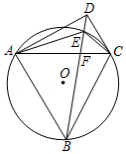
(3)求 的值.
如图, 的半径为 ,其内接锐角三角形 中, 、 、 所对的边分别是 、 、 .
(1)求证: ;
(2)若 , , ,利用(1)的结论求 的长和 的值.

试题篮
()