如图,ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,∠DCE=30°,若OE=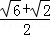 ,则正方形的面积为( )
,则正方形的面积为( )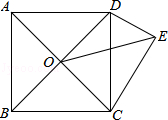
A.5 B.4 C.3 D.2
如图,在图1中, 、
、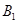 、
、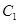 分别是等边△ABC的边BC、CA、AB的中点,在图2中,
分别是等边△ABC的边BC、CA、AB的中点,在图2中,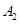 、
、 、
、 分别是△
分别是△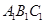 的边
的边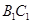 、
、 、
、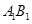 的中点,……,按此规律,则第n个图形中菱形的个数共有()个
的中点,……,按此规律,则第n个图形中菱形的个数共有()个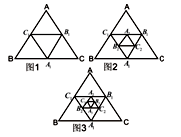
A.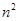 B.2n C.3n D.3n+1
B.2n C.3n D.3n+1
如图1,菱形ABCD的对角线交于点O,AC=2BD,点P是AO上一个动点,过点P作AC的垂线交菱形的边于M,N两点.设AP=x,△OMN的面积为y, 表示y与x的函数关系的图象大致如图2所示,则菱形的周长为()
| A.2 | B. |
C.4 | D.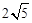 |
如图,有一块边长为6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是()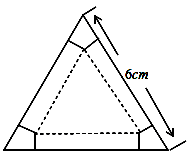
A.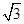 cm2 cm2 |
B. cm2 cm2 |
C.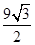 cm2 cm2 |
D.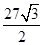 cm2 cm2 |
如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )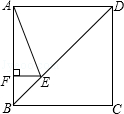
| A.1 | B.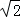 |
C.4﹣2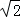 |
D.3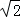 ﹣4 ﹣4 |
已知D、E、F分别为等腰△ABC边BC、CA、AB上的点,如果AB=AC,BD=2,CD=3,CE=4,AE=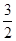 ,∠FDE=∠B,那么AF的长为()
,∠FDE=∠B,那么AF的长为()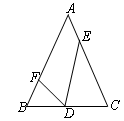
A.5.5B.4.5 C.4D.3.5
在平面直角坐标系内,直线y=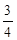 x+3与两坐标轴交于A、B两点,点O为坐标原点,若在该坐标平面内有以点P(不与点A、B、O重合)为顶点的直角三角形与Rt△ABO全等,且这个以点P为顶点的直角三角形与Rt△ABO有一条公共边,则所有符合条件的P点个数为( )
x+3与两坐标轴交于A、B两点,点O为坐标原点,若在该坐标平面内有以点P(不与点A、B、O重合)为顶点的直角三角形与Rt△ABO全等,且这个以点P为顶点的直角三角形与Rt△ABO有一条公共边,则所有符合条件的P点个数为( )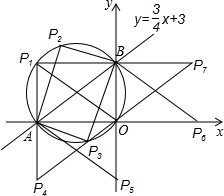
A.9个 B.7个 C.5个 D.3个
在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(4,3).平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M,N,直线m运动的时间为t(秒).设△OMN的面积为S,则能反映S与t之间函数关系的大致图象是()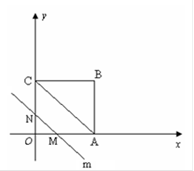
A.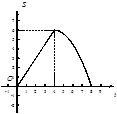 |
B.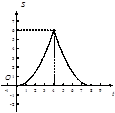 |
C.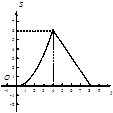 |
D. |
如图,直线y=x+1分别与x轴、y轴相交于点A、B,以点A为圆心,AB长为半径画弧交x轴于点A1,再过点A1作x轴的垂线交直线于点 B1,以点A为圆心,AB1长为半径画弧交x轴于点A2,……,按此做法进行下去,则点A8的坐标是()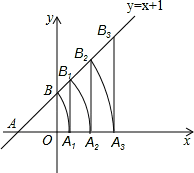
A.(15,0) B.(16,0) C.(8 ,0) D.(
,0) D.( ,0)
,0)
如图,在等腰三角形ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④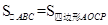 .其中所有正确结论的序号为( )
.其中所有正确结论的序号为( )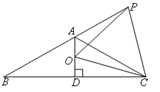
| A.①②③ | B.①②④ | C.①③④ | D.①②③④ |
将正方形对折后展开(图④是连续两次对折后再展开),再按图示方法折叠,能够得到一个直角三角形,且它的一条直角边等于斜边的一半.图①~④中这样的图形有()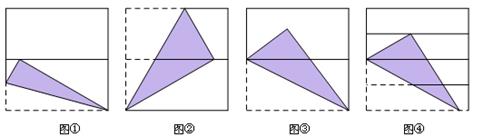
| A.4个 | B.3个 | C.2个 | D.1个 |
如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有()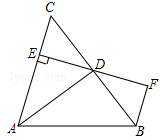
| A.4个 | B.3个 | C.2个 | D.1个 |
如图,一圆柱高8 cm,底面半径为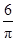 cm,一只蚂蚁从点
cm,一只蚂蚁从点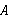 爬到点
爬到点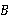 处吃食,要爬行的最短路程是()
处吃食,要爬行的最短路程是()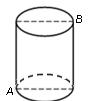
| A.6 cm | B.8 cm | C.10 cm | D.12 cm |
试题篮
()