如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,以O为圆心的半圆分别与AB、AC边相切于D、E两点,且O点在BC边上,则图中阴影部分面积S阴=()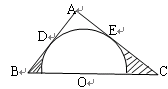
A、 B、
B、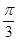
C、 5-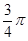 D、
D、
如图,在四边形ABCD中,∠ABC+∠DCB=90°,E、F分别是AD、BC的中点,分别以AB、CD为直径作半圆,这两个半圆面积的和为8π,则EF的长为 ()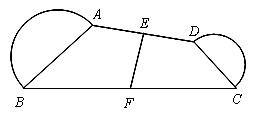
A.10B.8C.6D.4
如图,△ABC≌△ADE且∠ABC=∠ADE,∠ACB=∠AED,BC.DE交于点O.则下列四个结论中,①∠1=∠2;②BC=DE;③△ABD∽△ACE;④A.O、C.E四点在同一个圆上,一定成立的有( )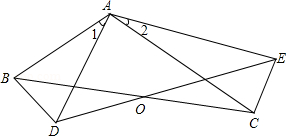
A. 1个 B. 2个 C. 3个 D. 4个
如图,已知∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上;
△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形.若OA1=1,则△A2015B2015A2016的边长为…()
| A.4028 | B.4030 | C.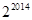 |
D.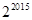 |
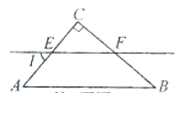
如图,AB∥CD,∠BAC与∠DCA的平分线相交于点G,GE⊥AC于点E,F为AC上的一点,且FA=FG=FC,GH⊥CD于H.下列说法:①AG⊥CG;②∠BAG=∠CGE;③S△AFG=S△CFG;④若∠EGH:∠ECH=2:7,则∠EGF=50度.其中正确的有( )
| A.①②③④ | B.②③④ | C.①③④ | D.①②④ |
如图,ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,∠DCE=30°,若OE=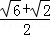 ,则正方形的面积为( )
,则正方形的面积为( )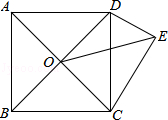
A.5 B.4 C.3 D.2
对于下列命题:
①对顶角相等;②同位角相等;③两直角相等; ④邻补角相等;
⑤有且只有一条直线垂直于已知直线;
⑥三角形一边上的中线把原三角形分成面积相等的两个三角形.
其中是真命题的共有
| A.2个 | B.3个 | C.4个 | D.5个 |
如图,在图1中, 、
、 、
、 分别是等边△ABC的边BC、CA、AB的中点,在图2中,
分别是等边△ABC的边BC、CA、AB的中点,在图2中,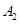 、
、 、
、 分别是△
分别是△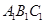 的边
的边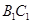 、
、 、
、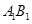 的中点,……,按此规律,则第n个图形中菱形的个数共有()个
的中点,……,按此规律,则第n个图形中菱形的个数共有()个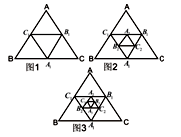
A.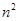 B.2n C.3n D.3n+1
B.2n C.3n D.3n+1
如图所示,一个正方形水池的四周恰好被4个正n边形地板砖铺满,则n等于( )
| A.4 | B.6 | C.8 | D.10 |
如图1,菱形ABCD的对角线交于点O,AC=2BD,点P是AO上一个动点,过点P作AC的垂线交菱形的边于M,N两点.设AP=x,△OMN的面积为y, 表示y与x的函数关系的图象大致如图2所示,则菱形的周长为()
| A.2 | B. |
C.4 | D.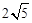 |
如图,在等腰三角形ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④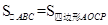 .其中所有正确结论的序号为( )
.其中所有正确结论的序号为( )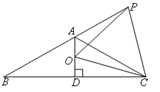
| A.①②③ | B.①②④ | C.①③④ | D.①②③④ |
将正方形对折后展开(图④是连续两次对折后再展开),再按图示方法折叠,能够得到一个直角三角形,且它的一条直角边等于斜边的一半.图①~④中这样的图形有()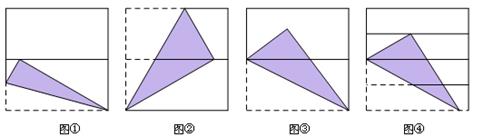
| A.4个 | B.3个 | C.2个 | D.1个 |
如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有()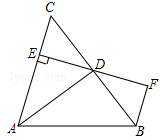
| A.4个 | B.3个 | C.2个 | D.1个 |
如图,一圆柱高8 cm,底面半径为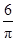 cm,一只蚂蚁从点
cm,一只蚂蚁从点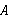 爬到点
爬到点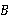 处吃食,要爬行的最短路程是()
处吃食,要爬行的最短路程是()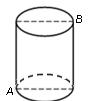
| A.6 cm | B.8 cm | C.10 cm | D.12 cm |
试题篮
()