我国古代数学著作《孙子算经》有"多人共车"问题:"今有三人共车,二车空;二人共车,九人步.问:人与车各几何?"其大意如下:有若干人要坐车,如果每3人坐一辆车,那么有2辆空车;如果每2人坐一辆车,那么有9人需要步行,问人与车各多少?设共有 人, 辆车,则可列方程组为
| A. |
|
B. |
|
| C. |
|
D. |
|
中国疫苗撑起全球抗疫"生命线" 中国外交部数据显示,截止2021年3月底,我国已无偿向80个国家和3个国际组织提供疫苗援助.预计2022年中国新冠疫苗产能有望达到50亿剂,约占全球产能的一半,必将为全球抗疫作出重大贡献.数据"50亿"用科学记数法表示为
| A. |
|
B. |
|
C. |
|
D. |
|
如图, 为 的直径,点 在 的延长线上, , 与 相切,切点分别为 , .若 , ,则 等于

| A. |
|
B. |
|
C. |
|
D. |
|
某市2018年底森林覆盖率为 .为贯彻落实"绿水青山就是金山银山"的发展理念,该市大力开展植树造林活动,2020年底森林覆盖率达到 ,如果这两年森林覆盖率的年平均增长率为 ,那么,符合题意的方程是
| A. |
|
B. |
|
| C. |
|
D. |
|
某校为推荐一项作品参加"科技创新"比赛,对甲、乙、丙、丁四项候选作品进行量化评分,具体成绩(百分制)如表:
|
项目 作品 |
甲 |
乙 |
丙 |
丁 |
|
创新性 |
90 |
95 |
90 |
90 |
|
实用性 |
90 |
90 |
95 |
85 |
如果按照创新性占 ,实用性占 计算总成绩,并根据总成绩择优推荐,那么应推荐的作品是
| A. |
甲 |
B. |
乙 |
C. |
丙 |
D. |
丁 |
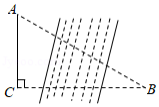
如图,某研究性学习小组为测量学校 与河对岸工厂 之间的距离,在学校附近选一点 ,利用测量仪器测得 , , .据此,可求得学校与工厂之间的距离 等于
| A. |
|
B. |
|
C. |
|
D. |
|
如图,用绳子围成周长为 的矩形,记矩形的一边长为 ,它的邻边长为 ,矩形的面积为 .当 在一定范围内变化时, 和 都随 的变化而变化,则 与 , 与 满足的函数关系分别是

| A. |
一次函数关系,二次函数关系 |
| B. |
反比例函数关系,二次函数关系 |
| C. |
一次函数关系,反比例函数关系 |
| D. |
反比例函数关系,一次函数关系 |
试题篮
()