初中数学填空题

在1：5000的地图上，A．B两地的图上距离为3cm，则A、B两地间实际距离为 m．

在一节数学实践活动课上，老师拿出三个边长都为4cm 的正方形硬纸板，他向同学们提出了这样一个问题：若将三个正方形纸板不重叠地放在桌面上，用一个圆形硬纸板将其盖住，这样的圆形硬纸板的最小直径应有多大？问题提出后，同学们经过讨论，大家觉得本题实际上就是求将三个正方形硬纸板无重叠地适当放置，圆形硬纸板能盖住时的最小直径．老师将同学们讨论过程中探索出的三种不同摆放类型的图形画在黑板上，如下图所示：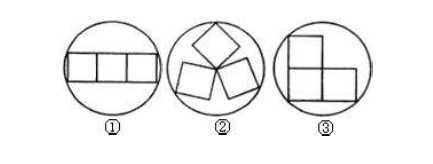

（1）通过计算（结果保留根号与π）．
（Ⅰ）图①能盖住三个正方形所需的圆形硬纸板最小直径应为_________
（Ⅱ）图②能盖住三个正方形所需的圆形硬纸板最小直径为___________
（Ⅲ）图③能盖住三个正方形所需的圆形硬纸板最小直径为___________
（2）其实上面三种放置方法所需的圆形硬纸板的直径都不是最小的，请你画出用圆形硬纸板盖住三个正方形时直径最小的放置方法，（只要画出示意图，不要求说明理由），并求出此时圆形硬纸板的直径．

如图，抛物线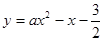与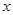轴正半轴交于点A（3，0）．以OA为边在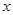轴上方作正方形OABC，延长CB交抛物线于点D，再以BD为边向上作正方形BDEF，点E的坐标是 ．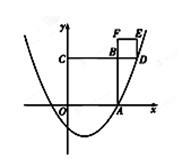

若a-b+c=0,a≠0, 则方程ax²+bx+c=0必有一个根是____________．

，则方程的解为___________．

已知二次函数y=ax²+bx+c（a≠0）的图象如图所示，给出以下结论：
①a+b+c＜0；②a-b+c＜0；③b+2a＜0；④abc＞0．其中所有正确结论的序号是______．

A．②③

B．①②

C．③④

D．①④

-（-2）的相反数是 ．

如图：从镜子中看到一钟表的时针和分针，此时的实际时刻是________．

根据下面给出的数轴，解答下面的问题：

（1）请你根据图中A、B两点的位置，分别写出它们所表示的有理数
A：__________ B： _____________ ；
（2）观察数轴，与点A的距离为4的点表示的数是：_____________ ；
（3）若将数轴折叠，使得A点与－3表示的点重合，则B点与数_ _表示的点重合；
（4）若数轴上M、N两点之间的距离为2016（M在N的左侧），且M、N两点经过（3）中折叠后互相重合，则M、N两点表示的数分别是：M：_______ N：_______．

（1）在数轴上表示下列有理数：，，0，3，－（－4），．

（2）各数用“<”号连接起来：________________________________________．

地球上的陆地面积约为149 000 000千米²，用科学记数法表示为 ．

如图所示是简单的数值计算程序，若开始输入x=-1，则最后输出的结果是 ．

数轴上的点P表示的数是－1，一只蚂蚁从点P出发，沿数轴向右爬行3个单位长度到达点Q，则点Q表示的数是 ．

苹果每千克元，梨每千克元，则整式表示购买 ．

直接写出计算结果：= ；= ； ．