题文
设函数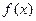 的定义域为D,若存在非零实数h使得对于任意
的定义域为D,若存在非零实数h使得对于任意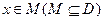 ,有
,有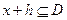 ,且
,且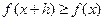 ,则称
,则称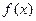 为M上的“h阶高调函数”。给出如下结论:
为M上的“h阶高调函数”。给出如下结论:
①若函数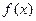 在R上单调递增,则存在非零实数h使
在R上单调递增,则存在非零实数h使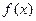 为R上的“
为R上的“ h阶高调函数”;
h阶高调函数”;
②若函数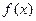 为R上的“h阶高调函数”,则
为R上的“h阶高调函数”,则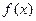 在R上单调递增;
在R上单调递增;
③若函数 为区间
为区间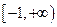 上的“h阶高诬蔑财函数”,则
上的“h阶高诬蔑财函数”,则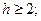
④若函数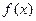 在R上的奇函数,且
在R上的奇函数,且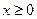 时,
时,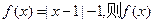 只能是R上的“4阶高调函数”。
只能是R上的“4阶高调函数”。
其中正确结论的序号为 ( )
A.① ③ ③ |
B.①④ | C.②③ | D.②④ |
推荐试卷








 粤公网安备 44130202000953号
粤公网安备 44130202000953号