题文
((本题14分)如图4,已知椭圆 的离心率为
的离心率为 ,以该椭圆上的点和椭圆的左右焦点F1,F2为顶点的三角形的周长为4
,以该椭圆上的点和椭圆的左右焦点F1,F2为顶点的三角形的周长为4 。一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D。
。一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D。
(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线PF1、PF2的斜率分别为 ;
;
(Ⅲ)是否存在常数 ,使得
,使得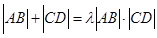 恒成立?若存在,求
恒成立?若存在,求 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
推荐试卷
((本题14分)如图4,已知椭圆 的离心率为
的离心率为 ,以该椭圆上的点和椭圆的左右焦点F1,F2为顶点的三角形的周长为4
,以该椭圆上的点和椭圆的左右焦点F1,F2为顶点的三角形的周长为4 。一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D。
。一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D。
(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线PF1、PF2的斜率分别为 ;
;
(Ⅲ)是否存在常数 ,使得
,使得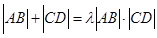 恒成立?若存在,求
恒成立?若存在,求 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
试题篮
()