题文
若正项数列 满足条件:存在正整数
满足条件:存在正整数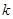 ,使得
,使得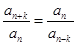 对一切
对一切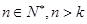 都成立,则称数列
都成立,则称数列 为
为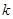 级等比数列.
级等比数列.
(1)已知数列 为2级等比数列,且前四项分别为
为2级等比数列,且前四项分别为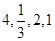 ,求
,求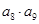 的值;
的值;
(2)若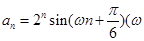 为常数),且
为常数),且 是
是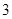 级等比数列,求
级等比数列,求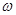 所有可能值的集合,并求
所有可能值的集合,并求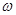 取最小正值时数列
取最小正值时数列 的前
的前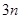 项和
项和 ;
;
(3)证明: 为等比数列的充要条件是
为等比数列的充要条件是 既为
既为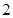 级等比数列,
级等比数列, 也为
也为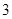 级等比数列.
级等比数列.
相关知识点
推荐试卷
若正项数列 满足条件:存在正整数
满足条件:存在正整数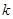 ,使得
,使得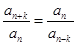 对一切
对一切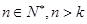 都成立,则称数列
都成立,则称数列 为
为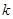 级等比数列.
级等比数列.
(1)已知数列 为2级等比数列,且前四项分别为
为2级等比数列,且前四项分别为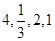 ,求
,求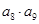 的值;
的值;
(2)若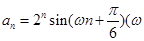 为常数),且
为常数),且 是
是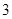 级等比数列,求
级等比数列,求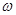 所有可能值的集合,并求
所有可能值的集合,并求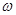 取最小正值时数列
取最小正值时数列 的前
的前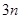 项和
项和 ;
;
(3)证明: 为等比数列的充要条件是
为等比数列的充要条件是 既为
既为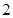 级等比数列,
级等比数列, 也为
也为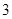 级等比数列.
级等比数列.
试题篮
()