题文
已知函数f（x）=x3﹣x2+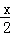
+
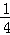，且存在x0∈（0，
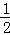），使f（x0）=x0．
（1）证明：f（x）是R上的单调增函数；
（2）设x1=0，xn+1=f（xn）；y1=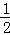，yn+1=f（yn），其中n=1，2，…，证明：xn＜xn+1＜x0＜yn+1＜yn；
（3）证明：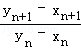
＜．
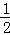推荐试卷
已知函数f（x）=x3﹣x2+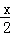+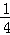，且存在x0∈（0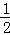，），使f（x0）=x0．
（1）证明：f（x）是R上的单调增函数；
（2）设x1=0，xn+1=f（xn）；y1=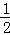，yn+1=f（yn），其中n=1，2，…，证明：xn＜xn+1＜x0＜yn+1＜yn；
（3）证明：＜．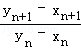
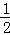试题篮
()
粤公网安备 44130202000953号
