如图,数轴上的A、B、C三点所表示的数分别是a、b、c,其中AB=BC,如果|a|>|b|>|c|,那么该数轴的原点O的位置应该在()
A.点A的左边
B.点A与点B之间
C.点B与点C之间
D.点B与点C之间或点C的右边
如图,每个底边为2的等腰三角形顶角的顶点都在反比例函数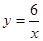 (x>0)的图像上,第1个等腰三角形顶角的顶点横坐标为1,第2个等腰三角形的顶点横坐标为3,……以此类推,用含n的式子表示第n个等腰三角形底边上的高为()
(x>0)的图像上,第1个等腰三角形顶角的顶点横坐标为1,第2个等腰三角形的顶点横坐标为3,……以此类推,用含n的式子表示第n个等腰三角形底边上的高为()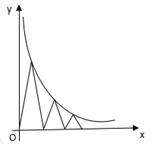
A.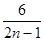 |
B.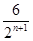 |
C. |
D.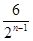 |
如图,直线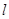 和双曲线
和双曲线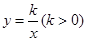 交于
交于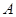 ,
,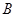 两点,
两点,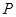 是线段
是线段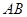 上的点(不与
上的点(不与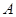 ,
,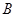 重合),过点
重合),过点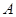 ,
,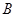 ,
,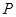 分别向
分别向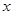 轴作垂线,垂足分别是
轴作垂线,垂足分别是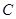 ,
, 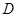 ,
,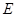 ,连接
,连接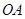 ,
,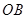 ,
,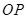 ,设
,设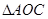 面积是
面积是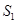 ,
,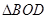 面积是
面积是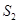 ,
,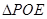 面积是
面积是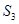 ,则().
,则().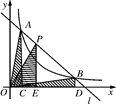
A.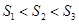 |
B.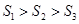 |
C. |
D. |
如图,在四边形ABCD中,E、F分别是AB、AD的中点.若EF=2,BC=5,CD=3,则tanC等于()
A. B.
B. C.
C. D.
D.
如果三角形满足一个角是另一个角的4倍,那么我们称这个三角形为“智慧三角形”.下列各组数据中,能作为一个智慧三角形三边长的一组是()
| A.1,2,3 | B.1,1,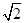 |
C.1,1,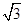 |
D.1,2,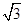 |
如图1,在△ABC中,∠ACB=90°,∠CAB=30°, △ABD是等边三角形,E是AB的中点,连结CE并延长交AD于F,如图2,现将四边形ACBD折叠,使D与C重合,HK为折痕,则sin∠ACH的值为()
A. |
B. |
C. |
D. |
如图,以坐标原点O为圆心的圆弧交y轴于点A(0,5),交x轴于点B,正方形CDEF内接于扇形AOB(其中C在y轴上、D在x轴上,E、F在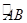 上),则正方形CDEF的边长为()
上),则正方形CDEF的边长为()
| A.3 | B. |
C.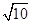 |
D.以上都不正确 |
如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH= BD;其中正确结论的是()
BD;其中正确结论的是()
| A.①②③ | B.①②④ | C.①③④ | D.②③④ |
如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积为s( ),则s(
),则s( )与t(s)的函数关系可用图像表示为()
)与t(s)的函数关系可用图像表示为()

如图,已知直线l1∥l2∥l3∥l4∥l5,相邻两条平行直线间的距离相等且为1,如果四边形ABCD的四个顶点在平行直线上,∠BAD=90°且AB=3AD,DC⊥l4,则四边形ABCD的面积是()
| A.9 | B.14 | C. |
D. |
如图,矩形A′B′C′D′是由矩形ABCD绕C点顺时针旋转而得,且点A、C、D′在同一条直线上,在Rt△ABC中,若AB=2,AD=2 ,则对角线AC旋转所扫过的扇形面积为()
,则对角线AC旋转所扫过的扇形面积为()
A. B.
B. C.
C. D.
D.
如图,在直角坐标系xoy中,已知 ,
, ,以线段
,以线段 为边向上作菱形
为边向上作菱形 ,且点
,且点 在y轴上.若菱形
在y轴上.若菱形 以每秒2个单位长度的速度沿射线
以每秒2个单位长度的速度沿射线 滑行,直至顶点
滑行,直至顶点 落在
落在 轴上时停止.设菱形落在
轴上时停止.设菱形落在 轴下方部分的面积为
轴下方部分的面积为 ,则表示
,则表示 与滑行时间
与滑行时间 的函数关系的图象为
的函数关系的图象为

如图,Rt△ABC中,∠C=90°,AC=3,BC=4.分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BDMC,四块阴影部分的面积分别为S1、S2、S3、S4.则S1+S2+S3+S4等于()
A.14 B.16 C.18 D.20
已知点A(-4,0),B(2,0).若点C在一次函数 的图象上,且△ABC是直角三角形,则点C的个数是( )
的图象上,且△ABC是直角三角形,则点C的个数是( )
| A.1 | B.2 | C.3 | D.4 |
试题篮
()