初中数学选择题

如图，正方形ABCD的对角线相交于O，点F在AD上，AD=3AF， △AOF的外接圆交AB于E，则的值为：（）

A．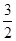

B．3

C．

D．2

在平面坐标系中，正方形ABCD的位置如图所示，点A的坐标为（1，0），点D的坐标为（0，2），延长CB交x轴于点A₁，作正方形A₁B₁C₁C，延长C₁B₁交x轴于点A₂，作正方形A₂B₂C₂C₁,………按这样的规律进行下去，第2012个正方形的面积为（）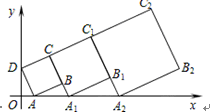

A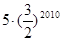．	B．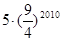
C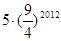．	D．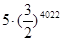

如图,在圆心角为90°的扇形MNK中，动点P从点M出发，沿运动，最后回到点M的位置。设点P运动的路程为x，P与M两点之间的距离为y，其图象可能是（）。

已知，+=0，则 =（）．

A．1

B．-2013

C．-1

D．2013

在平面直角坐标系中，孔明做走棋游戏，其走法是；棋子从原点起，第1步向右走1个单位，第2步向右走2个单位，第3步向上走1个单位，第4步向右走1个单位，……依此类推，第n步是：当n能被3整除时，则向上走1个单位；当n被3除，余数是1时，则向右走1个单位，当n被3除，余数为2时，则向右走2个单位，当他走完第100步时，棋子所处位置的坐标是(　　)

A．(66，34)

B．(67，33)

C．(100，33)

D．(99，34)

定义：直线l₁与l₂相交于点O，对于平面内任意一点M，点M到直线l₁、l₂的距离分别为p、q，则称有序实数对(p，q)是点M的“距离坐标”．根据上述定义，“距离坐标”是(1，2)的个数是(　　)

A．2

B．3

C．4

D．5

将一组数，，3，，，…，按下面的方法进行排列：
　　　　3　　　　
　　　　　　　　
…
若的位置记为(1，4)，的位置记为(2，3)，则这组数中最大的有理数的位置记为(　　)

A．(5，2)

B．(5，3)

C．(6，2)

D．(6，5)

将四根长度相等的细木条首尾相接，用钉子钉成四边形ABCD，转动这个四边形，使它形状改变．当∠B＝90°时，如图①，测得AC＝2．当∠B＝60°时，如图②，AC＝(　　)

A．

B．2

C．

D．

如图，矩形ABCD的面积为20cm2，对角线交于点O；以AB、AO为邻边作平行四边形AOC₁B，对角线交于点O₁；以AB、AO₁为邻边作平行四边形AO₁C₂B……依此类推，则平行四边形AO₄C₅B的面积为（　　）

A．cm²
B．cm²
C．cm²
D．cm²

对正方形ABCD进行分割，如图中图（1），其中E、F分别是BC、CD的中点，O、M、N、G分别是BD、OB、OD、EF的中点，沿分割线可以剪出一副“七巧板”，用这些部件可以拼出很多图案，图中图（2）就是用其中6块拼出的“飞机”．若△GOM的面积为1，则“飞机”的面积为________．

顺次连接矩形各边中点所得的四边形是（　　）

A．矩形

B．菱形

C．正方形

D．以上都不对

已知菱形ABCD的两条对角线AC、BD的乘积等于菱形的一条边长的平方，则菱形的一个钝角的大小是（　　）
A．165°
B．150°
C．135°
D．120°

如图，在矩形ABCD中，AB＝3，BC＝4，P为AD上一点，PE⊥AC于E，PF⊥BD于F，则PE＋PF的值为（　　）

A．

B．

C．2

D．

如图，正方形ABCD中，对角线AC、BD相交于点O，则图中的等腰三角形有(　　)

A．4个
B．6个
C．8个
D．10个

如图，在菱形ABCD中，AB＝5，∠BCD＝120°，则△ABC的周长等于(　　)

A．20

B．15

C．10

D．5