如图,正方形ABCD中,P为对角线上的点,PB=AB,连PC,作CE⊥CP交AP的延长线于E,AE交CD于F,交BC的延长线于G,则下列结论:①E为FG的中点;② ;③AD=DE;④CF=2DF.其中正确结论的个数是()
;③AD=DE;④CF=2DF.其中正确结论的个数是()
| A.1个 | B.2个 | C.3个 | D.4个 |
如图,已知抛物线 和直线
和直线 .我们约定:当
.我们约定:当 任取一值时,
任取一值时, 对应的函数值分别为
对应的函数值分别为 、
、 ,若
,若 ,取
,取 、
、 中的较小值记为
中的较小值记为 ;若
;若 ,记
,记 .
.
下列判断:
①当 时,
时, ;
;
②当 时,
时, 值越大,
值越大, 值越大;
值越大;
③使得 大于4的
大于4的 值不存在;
值不存在;
④若 ,则
,则 .其中正确的有 ()
.其中正确的有 ()
| A.1个 | B.2个 | C.3个 | D.4个 |
如图,动点P从点A出发,沿线段AB运动至点B后,立即按原路返回,点P在运动过程中速度不变,则以点B为圆心,线段BP长为半径的圆的面积S与点P的运动时间t的函数图象大致为( )
下列图形都是由同样大小的矩形按一定规律组成,其中第(1)个图形的面积为2 ,第(2)个图形的面积为8
,第(2)个图形的面积为8 ,第(3)个图形的面积为18
,第(3)个图形的面积为18 ,……,则第(10)个图形的面积为()
,……,则第(10)个图形的面积为()
A.196 |
B.200 |
C.216 |
D.256 |
实数x满足方程(x2+x)2-(x2+x)-2=0,则x2+x的值等于()
| A.2 | B. |
C.2或 |
D.1或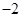 |
古希腊著名的毕达哥拉斯学派把1,3,6,10 …这样的数称为“三角形数”,而把1,4,9,16 …这样的数称为“正方数”. 从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )
| A.20=6+14 | B.25=9+16 | C.36=16+20 | D.49=21+28 |
如图,分别是由若干个完全相同的小正方体组成的一个几何体的主视图和俯视图,则组成这个几何体的小正方体的个数是()
| A.2个或3个 | B.3个或4个 | C.4个或5个 | D.5个或6个 |
如图,在四边形ABCD中,∠ABC+∠DCB=90°,E、F分别是AD、BC的中点,分别以AB、CD为直径作半圆,这两个半圆面积的和为8π,则EF的长为 ()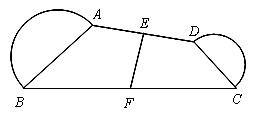
A.10B.8C.6D.4
如图,在直角坐标系中,将矩形OABC沿OB对折,使点A落在点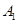 处,已知OA=
处,已知OA=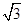 ,AB=1,则点
,AB=1,则点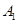 的坐标是()
的坐标是()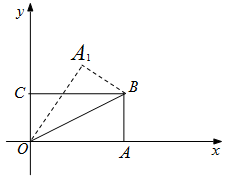
A.(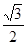 , ,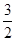 ) ) |
B.(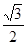 ,3) ,3) |
C.(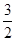 , ,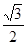 ) ) |
D.(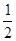 , ,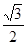 ) ) |
如图,已知D、E、F分别是等边△ABC的边AB、BC、AC上的点,且DE⊥BC、EF⊥AC、FD⊥AB,则下列结论不成立的是( )
A.△DEF是等边三角形
B.△ADF≌△BED≌△CFE
C.DE= AB
AB
D.S△ABC=3S△DEF
如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )
A. |
B. |
C. |
D.不能确定 |
如图,点B、C、E在同一条直线上,△ABC与△CDE都是等边三角形,则下列结论不一定成立的是( )
A.△ACE≌△BCD B.△BGC≌△AFC
C.△DCG≌△ECF D.△ADB≌△CEA
边长为a的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点,顺次连接又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图),…,按此方式依次操作,则第6个正六边形的边长为( )
A. |
B. |
C. |
D. |
试题篮
()