已知:二次函数 为常数).
(1)请写出该二次函数的三条性质;
(2)在同一直角坐标系中,若该二次函数的图象在 的部分与一次函数 的图象有两个交点,求 的取值范围.
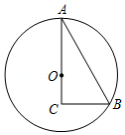
如图,在 中, , , ,以边 上一点 为圆心, 为半径的 经过点 .
(1)求 的半径;
(2)点 为劣弧 中点,作 ,垂足为 ,求 的长;
(3)在(2)的条件下,连接 ,求 的值.
列方程解应用题:
中华优秀传统文化是中华民族的“根”和“魂”.为传承优秀传统文化,某校购进《西游记》和《三国演义》若干套,其中每套《西游记》的价格比每套《三国演义》的价格多40元,用3200元购买《三国演义》的套数是用2400元购买《西游记》套数的2倍,求每套《三国演义》的价格.
第一盒中有2个白球、1个黄球,第二盒中有1个白球、1个黄球,这些球除颜色外无其他差别.分别从每个盒中随机取出1个球,求取出的2个球中有1个白球、1个黄球的概率.
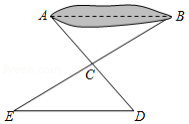
如图,有一池塘,要测池塘两端 , 的距离,可先在平地上取一个点 ,从点 不经过池塘可以直接到达点 和 .连接 并延长到点 ,使 .连接 并延长到点 ,使 .连接 ,那么量出 的长就是 , 的距离.为什么?
如图,在平面直角坐标系 中,抛物线 过点 ,与抛物线 的一个交点为 ,且点 的横坐标为2,点 、 分别是抛物线 、 上的动点.
(1)求抛物线 对应的函数表达式;
(2)若以点 、 、 、 为顶点的四边形恰为平行四边形,求出点 的坐标;
(3)设点 为抛物线 上另一个动点,且 平分 .若 ,求出点 的坐标.

如图,在平面直角坐标系 中,函数 的图象与函数 的图象相交于点 ,并与 轴交于点 .点 是线段 上一点, 与 的面积比为 .
(1) , ;
(2)求点 的坐标;
(3)若将 绕点 逆时针旋转,得到△ ,其中点 落在 轴负半轴上,判断点 是否落在函数 的图象上,并说明理由.

如图,海上观察哨所 位于观察哨所 正北方向,距离为25海里.在某时刻,哨所 与哨所 同时发现一走私船,其位置 位于哨所 北偏东 的方向上,位于哨所 南偏东 的方向上.
(1)求观察哨所 与走私船所在的位置 的距离;
(2)若观察哨所 发现走私船从 处以16海里 小时的速度向正东方向逃窜,并立即派缉私艇沿北偏东 的方向前去拦截,求缉私艇的速度为多少时,恰好在 处成功拦截.(结果保留根号)
(参考数据: , , ,

试题篮
()