初中数学计算题

如下图，已知反比例函数(k＞0)的图象经过点A(1，m)，过点A作AB⊥y轴于点B，且△AOB的面积为1．

(1)求m，k的值；
(2)若一次函数y＝nx＋2(n≠0)的图象与反比例函数的图象有两个不同的公共点，求实数n的取值范围．

如下图，已知在平面直角坐标系xOy中，O是坐标原点，点A(2，5)在反比例函数的图象上，过点A的直线y＝x＋b交x轴于点B．

(1)求k和b的值；
(2)求△AOB的面积．

已知反比例函数(k≠－1)，且该函数的图象经过点(2，－1)．
(1)求k的值；
(2)若点(1，a)在该函数的图象上，求a的值．

将代入反比例函数中，所得的函数值为y₁，再将x＝y₁＋1代入函数中，所得的函数值为y₂，再将x＝y₂＋1代入函数中，所得的函数值为y₃……如此下去，求y₂₀₁₄的值．

已知y＝y₁＋y₂，y₁与x成正比例，y₂与x²成反比例，并且当x＝1与x＝2时，y的值都等于7，求x＝－1时，y的值．

若函数是反比例函数，求m的值．

当k为何值时，是反比例函数？

利用一面墙（墙的长度不限），另三边用58m长的篱笆围成一个面积为200m²的矩形场地，求矩形的长和宽．

计算：．

如图，已知反比例函数的图象与一次函数的图象相交于点A（1，4）和点B（n，）．

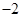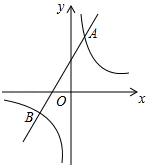
（1）求反比例函数和一次函数的解析式；
（2）当一次函数的值小于反比例函数的值时，直接写出x的取值范围．

如图，某数学兴趣小组在活动课上测量学校旗杆的高度．已知小亮站着测量 ，眼睛与地面的距离（AB）是1．7米，看旗杆顶部E的仰角为30°；小敏蹲着测量，眼睛与地面的距离（CD）是0．7米，看旗杆顶部E的仰角为45°．两人相距5米且位于旗杆同侧（点B、D、F在同一直线上）．

（1）求小敏到旗杆的距离DF．（结果保留根号）
（2）求旗杆EF的高度．（结果保留整数．参考数据：，）

计算： $\sqrt{8}+|2-3|-（\frac{1}{3}{）}^{-1}-（2015+\sqrt{2}{）}^0$

计算：17－2³÷（－2）×3

阅读材料：关于三角函数还有如下的公式：Sin（αβ）=sinαcosβcosαsinβ
tan（αβ）=
利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值，
例：tan15°=tan（45°-30°）
=
=
=

根据以上阅读材料，请选择适当的公式解答下面的问题：
（1）计算sin15°；
（2）我县体育场有一移动公司的信号塔，小明想利用所学的数学知识来测量该塔的高度，小华站在离塔底A距离7米的C处，测得塔顶的仰角为75°，小华的眼睛离地面的距离DC为1.62米，请帮助小华求出该信号塔的高度．（精确到0.1米，参考数据：）

（本小题满分12分）清明节期间，两位同学到某超市调查一种进价为2元／只的粽子的情况。请根据对话提供的信息，解答以下问题：

（1）当销售单价是多少元时，每天的销售利润可达到800元？
（2）当销售单价是多少元时，每天的销售利润可达到最大？
注：销售利润＝销售量×（销售单价－进价）.