初中数学计算题

（本小题满分8分）如下图，过正方形ABCD的顶点B作直线l，过点A，C作直线l的垂线，垂足分别为E，F，直线AE交CD于点G.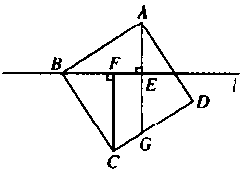

（1）求证：△ABE≌△ABE；
（2）若∠CBF＝65°，求∠AGC的度数.

在一个不透明的口袋里装有四个分别标有1、2、3、4的小球，它们的形状、大小等完全相同．小明先从口袋里随机取出一个小球，记下数字为x；小红在剩下的三个小球中随机取出一个小球，记下数字为y．小明、小红约定做一个游戏，其规则是：若x、y满足xy＞6，则小明胜；若x、y满足xy＜6，则小红胜．这个游戏规则公平吗？说明你的理由；若不公平，怎样修改游戏规则才对双方公平？

如图，已知⊙O的直径AB与弦CD相交于点E，AB⊥CD，⊙O的切线BF与弦AD的延长线相交于点F．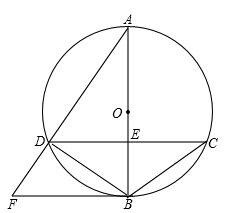

（1）求证：CD∥BF；
（2）若⊙O的半径为5，cos∠BCD=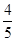，求线段AD的长．

化简：

如图在△ABC中，BE平分∠ABC，∠C=90°，D在AB边上，以DB为直径的半圆O经过点E交BC于点F．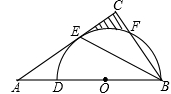

（1）求证：AC是⊙O的切线；
（2）已知sinA=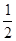，⊙O的半径为4，求图中阴影部分的面积．

如图，△ABC中，AB=AC，∠BAC=40°，将△ABC绕点A按逆时针方向旋转100°，得到△ADE，连接BD、CE，两线交于点F．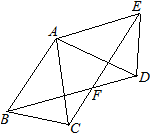

（1）求证：△ABD≌△ACE；
（2）求证：四边形ABFE是菱形．

计算：．

如图，O是△ABC的内心，BO的延长线和△ABC的外接圆相交于D，连接DC、DA、OA、OC，四边形OADC为平行四边形。

（1）求证：△BOC≌△CDA
（2）若AB=2，求阴影部分的面积。

计算：．

列方程或方程组解应用题：
周末小明和爸爸准备一起去商场购买一些茶壶和一些茶杯，了解情况后发现甲、乙两家商场都在出售两种同样品牌的茶壶和茶杯，定价相同，茶壶每把定价30元，茶杯每只定价5元，且两家都有优惠．甲商场买一送一大酬宾（买一把茶壶送一只茶杯）；乙商场全场九折优惠．小明的爸爸需茶壶5把，茶杯若干只（不少于5只）．当去两家商场付款一样时，求需要购买茶杯的数量．

计算：．

计算：．

已知：如图，在矩形ABCD中，E是BC边上一点，DE平分，EF∥DC交AD边于点F，连结BD．

（1）求证：四边形FECD是正方形；
（2）若求的值．

列方程或方程组解应用题：
几个小伙伴打算去音乐厅看演出，他们准备用360元钱购买门票．下面是两个小伙伴的对话：

根据对话中的信息，请你求出这些小伙伴的人数．

解分式方程：．