如图①,在四边形 中, 于点 , ,点 为 中点, 为线段 上的点,且 .
(1)求证: 平分 ;
(2)若 ,连接 ,当四边形 为平行四边形时,求线段 的长;
(3)如图②,若点 为 的中点,连接 、 ,求证: .

传统的端午节即将来临,某企业接到一批粽子生产任务,约定这批粽子的出厂价为每只4元,按要求在20天内完成.为了按时完成任务,该企业招收了新工人,设新工人李明第 天生产的粽子数量为 只, 与 满足如下关系:
(1)李明第几天生产的粽子数量为280只?
(2)如图,设第 天生产的每只粽子的成本是 元, 与 之间的关系可用图中的函数图象来刻画.若李明第 天创造的利润为 元,求 与 之间的函数表达式,并求出第几天的利润最大?最大利润是多少元?(利润 出厂价 成本)

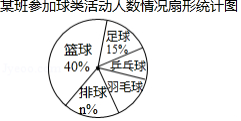
为了推进球类运动的发展,某校组织校内球类运动会,分篮球、足球、排球、羽毛球、乒乓球五项,要求每位学生必须参加一项并且只能参加一项,某班有一名学生根据自己了解的班内情况绘制了如图所示的不完整统计表和扇形统计图.
某班参加球类活动人数统计表
|
项目 |
篮球 |
足球 |
排球 |
羽毛球 |
乒乓球 |
|
人数 |
|
6 |
8 |
6 |
4 |
请根据图表中提供的信息,解答下列问题:
(1)图表中 , ;
(2)若该校学生共有1000人,则该校参加羽毛球活动的人数约为 人;
(3)该班参加乒乓球活动的4位同学中,有3位男同学(分别用 , , 表示)和1位女同学(用 表示),现准备从中选出两名同学参加双打比赛,用树状图或列表法求出恰好选出一男一女的概率.
知识改变世界,科技改变生活.导航装备的不断更新极大方便了人们的出行.如图,某校组织学生乘车到黑龙滩(用 表示)开展社会实践活动,车到达 地后,发现 地恰好在 地的正北方向,且距离 地13千米,导航显示车辆应沿北偏东 方向行驶至 地,再沿北偏西 方向行驶一段距离才能到达 地,求 、 两地的距离.(参考数据: , ,

在边长为 1 个单位长度的正方形网格中建立如图所示的平面直角坐标系, 的顶点都在格点上, 请解答下列问题:
(1) 作出 向左平移 4 个单位长度后得到的△ ,并写出点 的坐标;
(2) 作出 关于原点 对称的△ ,并写出点 的坐标;
(3) 已知 关于直线 对称的△ 的顶点 的坐标为 ,请直接写出直线 的函数解析式 .

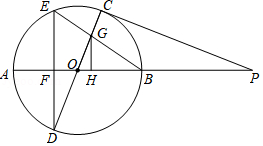
如图,已知 , 是 的直径,过点 作 的切线交 的延长线于点 , 的弦 交 于点 ,且 .
(1)求证: ;
(2)连接 交 于点 ,过点 作 于点 ,若 , ,求 的长.
一次函数 的图象经过点 , .
(1)求该一次函数的解析式;
(2)如图,该一次函数的图象与反比例函数 的图象相交于点 , , , ,与 轴交于点 ,且 ,求 的值.

如图,甲建筑物 ,乙建筑物 的水平距离 为 ,且乙建筑物的高度是甲建筑物高度的6倍,从 , , 在同一水平线上)点测得 点的仰角为 ,测得 点的仰角为 ,求这两座建筑物顶端 、 间的距离(计算结果用根号表示,不取近似值).

某图书馆计划选购甲、乙两种图书.已知甲图书每本价格是乙图书每本价格的2.5倍,用800元单独购买甲图书比用800元单独购买乙图书要少24本.
(1)甲、乙两种图书每本价格分别为多少元?
(2)如果该图书馆计划购买乙图书的本数比购买甲图书本数的2倍多8本,且用于购买甲、乙两种图书的总经费不超过1060元,那么该图书馆最多可以购买多少本乙图书?
为了解某中学学生课余生活情况,对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计.现从该校随机抽取 名学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名学生只能选择其中一项).并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图.由图中提供的信息,解答下列问题:
(1)求 的值;
(2)若该校学生共有1200人,试估计该校喜爱看电视的学生人数;
(3)若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名学生,求恰好抽到2名男生的概率.

结合西昌市创建文明城市要求,某小区业主委员会决定把一块长 ,宽 的矩形空地建成花园小广场,设计方案如图所示,阴影区域为绿化区(四块绿化区为全等的直角三角形),空白区域为活动区,且四周出口宽度一样,其宽度不小于 ,不大于 ,预计活动区造价60元 ,绿化区造价50元 ,设绿化区域较长直角边为 .
(1)用含 的代数式表示出口的宽度;
(2)求工程总造价 与 的函数关系式,并直接写出 的取值范围;
(3)如果业主委员会投资28.4万元,能否完成全部工程?若能,请写出 为整数的所有工程方案;若不能,请说明理由.
(4)业主委员会决定在(3)设计的方案中,按最省钱的一种方案,先对四个绿化区域进行绿化,在实际施工中,每天比原计划多绿化 ,结果提前4天完成四个区域的绿化任务,问原计划每天绿化多少 .

阅读材料:基本不等式 ,当且仅当 时,等号成立.其中我们把 叫做正数 、 的算术平均数, 叫做正数 、 的几何平均数,它是解决最大(小 值问题的有力工具.
例如:在 的条件下,当 为何值时, 有最小值,最小值是多少?
解: , 即是
当且仅当 即 时, 有最小值,最小值为2.
请根据阅读材料解答下列问题
(1)若 ,函数 ,当 为何值时,函数有最值,并求出其最值.
(2)当 时,式子 成立吗?请说明理由.
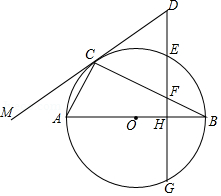
已知: 内接于 , 是 的直径,作 于 ,交 于 ,延长 交直线 于 ,且 ,求证:
(1) 是 的切线;
(2) 是等腰三角形.
试题篮
()