题文
我们知道,一元二次方程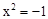 没有实数根,即不存在一个实数的平方等于
没有实数根,即不存在一个实数的平方等于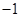 .若我们规定一个新数“
.若我们规定一个新数“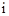 ”,使其满足
”,使其满足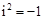 (即方程
(即方程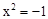 有一个根为
有一个根为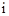 ).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有
).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有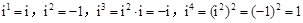 ,从而对于任意正整数
,从而对于任意正整数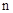 ,我们可以得到
,我们可以得到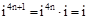 ,同理可得
,同理可得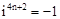 ,
,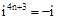 ,
,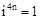 .那么
.那么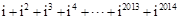 的值为 .
的值为 .
相关知识点
推荐试卷
我们知道,一元二次方程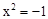 没有实数根,即不存在一个实数的平方等于
没有实数根,即不存在一个实数的平方等于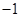 .若我们规定一个新数“
.若我们规定一个新数“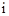 ”,使其满足
”,使其满足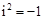 (即方程
(即方程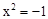 有一个根为
有一个根为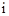 ).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有
).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有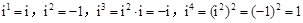 ,从而对于任意正整数
,从而对于任意正整数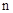 ,我们可以得到
,我们可以得到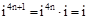 ,同理可得
,同理可得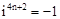 ,
,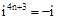 ,
,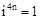 .那么
.那么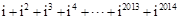 的值为 .
的值为 .
试题篮
()