如图,正方形的边长为4,剪去四个角后成为一个正八边形,则可求出此正八边形的外接圆直径 ,根据我国魏晋时期数学家刘徽的"割圆术"思想,如果用此正八边形的周长近似代替其外接圆周长,便可估计 的值,下面 及 的值都正确的是

| A. |
, |
| B. |
, |
| C. |
, |
| D. |
, |
在平面直角坐标系中,点 , .以 为一边在第一象限作正方形 ,则对角线 所在直线的解析式为
| A. |
|
B. |
|
C. |
|
D. |
|
某学校初一年级学生来自农村,牧区,城镇三类地区,下面是根据其人数比例绘制的扇形统计图,由图中的信息,得出以下3个判断,错误的有
①该校初一学生在这三类不同地区的分布情况为 .
②若已知该校来自牧区的初一学生为140人,则初一学生总人数为1080人.
③若从该校初一学生中抽取120人作为样本,调查初一学生父母的文化程度,则从农村、牧区、城镇学生中分别随机抽取30、20、70人,样本更具有代表性.

| A. |
3个 |
B. |
2个 |
C. |
1个 |
D. |
0个 |
甲、乙两人在一条长400米的直线跑道上同起点、同终点、同方向匀速跑步,先到终点的人原地休息.已知甲先出发3秒,在跑步过程中,甲、乙两人间的距离 (米 与乙出发的时间 (秒 之间的函数关系如图所示,则下列结论正确的个数是
①乙的速度为5米 秒;
②离开起点后,甲、乙两人第一次相遇时,距离起点12米;
③甲、乙两人之间的距离超过32米的时间范围是 ;
④乙到达终点时,甲距离终点还有68米.

| A. |
4 |
B. |
3 |
C. |
2 |
D. |
1 |
已知抛物线 上的部分点的横坐标 与纵坐标 的对应值如表:
|
|
|
|
0 |
1 |
2 |
3 |
|
|
|
|
3 |
0 |
|
|
3 |
|
以下结论正确的是
| A. |
抛物线 的开口向下 |
| B. |
当 时, 随 增大而增大 |
| C. |
方程 的根为0和2 |
| D. |
当 时, 的取值范围是 |
如图,点 , 在以 为直径的半圆上,且 ,点 是 上任意一点,连接 、 .则 的度数为
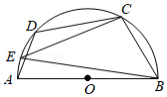
| A. |
|
B. |
|
C. |
|
D. |
|
五一期间,某地相关部门对观光游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整),根据图中的信息,下列结论错误的是
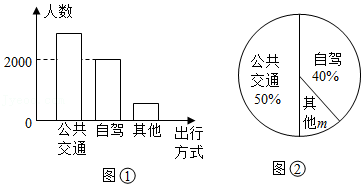
| A. |
本次抽样调查的样本容量是5000 |
| B. |
扇形统计图中的 为 |
| C. |
若五一期间观光的游客有50万人,则选择自驾方式出行的大约有20万人 |
| D. |
样本中选择公共交通出行的有2400人 |
如图,在平面直角坐标系中,菱形 的边 与 轴平行, , 两点纵坐标分别为4,2,反比例函数 经过 , 两点,若菱形 面积为8,则 值为

| A. |
|
B. |
|
C. |
|
D. |
|
已知一次函数 过点 ,则下列结论正确的是
| A. |
随 增大而增大 |
| B. |
|
| C. |
直线过点 |
| D. |
与坐标轴围成的三角形面积为2 |
试题篮
()