如图, 为矩形 的对角线,已知 , ,点 沿折线 以每秒1个单位长度的速度运动(运动到 点停止),过点 作 于点 ,则 的面积 与点 运动的路程 间的函数图象大致是

| A. |
|
B. |
|
| C. |
|
D. |
|
如图,已知二次函数 的图象与 轴交于 ,顶点是 ,则以下结论:① ;② ;③若 ,则 或 ;④ .其中正确的有 个.

| A. |
1 |
B. |
2 |
C. |
3 |
D. |
4 |
如图,在 的正方形网格中,每个小正方形的边长都为1, 为 与正方形网格线的交点,下列结论正确的是
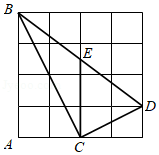
| A. |
|
B. |
|
C. |
|
D. |
|
如图, 中, , , .点 为 内一点,且满足 .当 的长度最小时, 的面积是
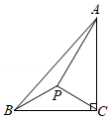
| A. |
3 |
B. |
|
C. |
|
D. |
|
二次函数 的图象的一部分如图所示.已知图象经过点 ,其对称轴为直线 .下列结论:
① ;
② ;
③ ;
④若抛物线经过点 ,则关于 的一元二次方程 的两根分别为 ,5.
上述结论中正确结论的个数为

| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |
筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1.筒车盛水桶的运行轨道是以轴心 为圆心的圆,如图2.已知圆心 在水面上方,且 被水面截得的弦 长为6米, 半径长为4米.若点 为运行轨道的最低点,则点 到弦 所在直线的距离是

| A. |
1米 |
B. |
米 |
C. |
2米 |
D. |
米 |
已知 为实数,规定运算: , , , , , .按上述方法计算:当 时, 的值等于
| A. |
|
B. |
|
C. |
|
D. |
|
已知锐角 ,如图,按下列步骤作图:①在 边取一点 ,以 为圆心, 长为半径画 ,交 于点 ,连接 .②以 为圆心, 长为半径画 ,交 于点 ,连接 .则 的度数为
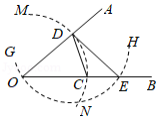
| A. |
|
B. |
|
C. |
|
D. |
|
已知在 中, , , ,点 为边 上的动点,点 为边 上的动点,则线段 的最小值是
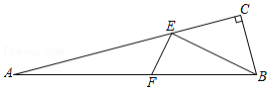
| A. |
|
B. |
|
C. |
|
D. |
|
已知函数 ,则下列说法不正确的个数是
①若该函数图像与 轴只有一个交点,则 ;
②方程 至少有一个整数根;
③若 ,则 的函数值都是负数;
④不存在实数 ,使得 对任意实数 都成立.
| A. |
0 |
B. |
1 |
C. |
2 |
D. |
3 |
如图1,矩形 中,点 为 的中点,点 沿 从点 运动到点 ,设 , 两点间的距离为 , ,图2是点 运动时 随 变化的关系图象,则 的长为
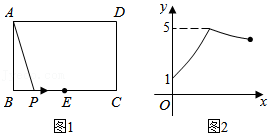
| A. |
4 |
B. |
5 |
C. |
6 |
D. |
7 |
如图, 的顶点 , ,点 在 轴的正半轴上,延长 交 轴于点 .将 绕点 顺时针旋转得到△ ,当点 的对应点 落在 上时, 的延长线恰好经过点 ,则点 的坐标为

| A. |
, |
B. |
, |
C. |
, |
D. |
, |
如图,等腰 中,顶角 ,用尺规按①到④的步骤操作:
①以 为圆心, 为半径画圆;
②在 上任取一点 (不与点 , 重合),连接 ;
③作 的垂直平分线与 交于 , ;
④作 的垂直平分线与 交于 , .
结论Ⅰ:顺次连接 , , , 四点必能得到矩形;
结论Ⅱ: 上只有唯一的点 ,使得 .
对于结论Ⅰ和Ⅱ,下列判断正确的是

| A. |
Ⅰ和Ⅱ都对 |
B. |
Ⅰ和Ⅱ都不对 |
C. |
Ⅰ不对Ⅱ对 |
D. |
Ⅰ对Ⅱ不对 |
试题篮
()