初中数学计算题

如图，在矩形ABCD中，E、F分别是边AB、CD的中点，连接AF，CE．

（1）求证：△BEC≌△DFA；
（2）求证：四边形AECF是平行四边形．

（1）计算：（）^﹣1﹣（﹣1）²⁰¹⁵﹣（π﹣3.14）⁰+|﹣5|
（2）先化简÷（a+1）+，然后在﹣1，1，2中选一恰当值代入求值．

某校组织若干名学生外出参观，住宿时发现，若每个房间住4人将有20人无法安排；若每个房间住8人，则有一个房间的人不空也不满．问这批学生有多少人？共有几个房间？

已知坐标平面内的三个点A（1，3），B（3，1），O（0，0），求△ABO的面积．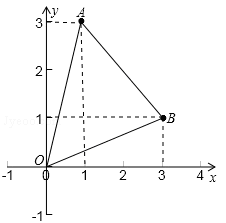

计算

一只不透明的袋子里共有4个球，其中3个白球，1个红球，它们除颜色外均相同．
（1）从袋子中随机摸出一个球是白球的概率是多少？
（2）从袋子中随机摸出一个球，不放回袋子，摇匀袋子后再摸一个球，请用列表或画树状图的方法，求出两次摸出的球都是白球的概率．

如图，在△ABC中，D、E分别是AB、AC的中点，BE=2DE，延长DE到点F，使得EF=BE，连接CF．

（1）求证：四边形BCFE是菱形；
（2）若CE=4，∠BCF=120°，求菱形BCFE的面积．

如图，已知EF∥AD，∠1=∠2，∠BAC=70°，求∠AGD的度数，下面给出了求∠AGD的度数的过程，将此补充完整并在括号里填写依据．

解∵EF∥AD（已知）
∴∠2= （ ）
又∵∠1=∠2（已知）
∴∠1=∠3（等式性质或等量代换）
∴AB∥ （ ）
∴∠BAC+ =180°（ ）
又∵∠BAC=70°（已知）
∴∠AGD= （ ）

已知2m=a，2n=b（m，n为正整数）．
（1）= ，= ．
（2）求的值．

（－）（+）

化简：3（+2﹣1）﹣（3+4﹣2）．

计算：．

42×（－）÷－（－12）÷（－4）．

如图，已知在平行四边形ABCD中，E、F分别是边AD、BC上的点，且DE=BF，过E、F两点作直线，分别与CD、AB的延长线相交于点M、N，连接CE、AF．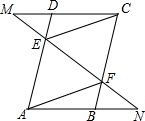

求证：（1）四边形AFCE是平行四边形；
（2）△MEC≌△NFA．

计算：
（1）（2﹣3+6）÷2
（2）