初中数学计算题

计算：

A、B两站间的路程为448千米，一列慢车从A站出发，每小时行驶60千米；一列快车从B站出发，每小时行驶80千米，问：
（1）两车同时开出，相向而行，出发后多少小时相遇？
（2）两车相向而行，慢车先开出28分钟，快车开出后多少小时两车相遇？

某校甲、乙、丙同学一同调查了北京的二环路、三环路、四环路高峰段的车流量．
甲同学说：“二环路车流量为每小时10000辆”．
乙同学说：“四环路比三环路车流量每小时多2000辆”．
丙同学说：“三环路车流量的3倍与四环路车流量的差是二环路车流量的2倍”．
请根据他们提供的信息，求出高峰时段三环路、四环路的车流量各是多少？

．中国唐朝“李白沽酒”的故事．
李白无事街上走，提着酒壶去买酒．遇店加一倍，见花喝一斗．
三遇店和花，喝光壶中酒．试问壶中原有多少酒？

（原创题）小明在汽车上，汽车匀速前进，他看到路旁公里牌上是一个两位数，一小时后，他又看见公里牌上的两位数恰好是前次两位数个、十位数字互换了一下，又过了一个小时，公里牌上是一个三位数，它是第一次看见的两位数中间加了一个零，求汽车的速度．

（原创题）阅读下列材料再解方程：
│x+2│=3，我们可以将x+2视为一个整体，由于绝对值为3的数有两个，所以x+2=3或x+2=－3，解得x=1或－5．
请按照上面解法解方程x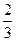－│x+1│=1．

（经典题）七年级（2）班的一个综合实践活动小组去A、B两个超市调查去年和今年“五·一”期间的销售情况，下图是调查后小敏与其他两位同学进行交流的情景．根据他们的对话，求A，B两个超市“五·一”期间的销售额（只需列出方程即可）．

用方程表示数量关系:
（1）若数的2倍减去1等于这个数加上5．
（2）一种商品按成本价提高40%后标价，再打8折销售，售价为240元，设这件商品的成本价为x元．
（3）甲，乙两人从相距60千米的两地同时出发，相向而行2小时后相遇，甲每小时比乙少走4千米，设乙的速度为x千米/时．

已知方程（m－2）x^|m|－1+3=m－5是关于x的一元一次方程，求m的值，并写出其方程．

解下列方程：
（1）4x－7=13；（2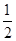）x－2=4+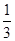x
（3）0.3x+1.2－2x=1.2－27x（4）40×10%·x－5=100×20%+12x

如图，在三角形ABC中，AB=AC=13，AD、BE是高，AD=12。
（1）求BC的长；（3分。）
（2）求DE的长；（2分。）
（3）求BE的长。（2分。）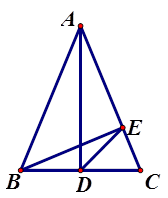

（每小题4分，共8分）计算：
①②

、图a是一个长为2 m、宽为2 n的长方形, 沿图中虚线用剪刀均分成四块小长方形, 然后按图b的形状拼成一个正方形.

(1) 写出图b中的阴影部分的正方形的边长；
(2) 写出图b中阴影部分的面积：
(3)观察图b写出下列三个代数式之间的等量关系；
根据（3）题中的等量关系，解决如下问题：若，求

、一块700的芯片上能集成10亿个元件，每一个这样的元件占多少平方毫米？（用科学记数法表示）.

、 若与M的乘积等于21，求M