旅游公司在景区内配置了50辆观光车供游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金 (元)是5的倍数.发现每天的营运规律如下:当 不超过100元时,观光车能全部租出;当 超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.
(1)优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入 租车收入 管理费)
(2)当每辆车的日租金为多少元时,每天的净收入最多?
如图,直立于地面上的电线杆 ,在阳光下落在水平地面和坡面上的影子分别是 、 ,测得 米, 米, ,在 处测得电线杆顶端 的仰角为 ,试求电线杆的高度(结果保留根号)

今年5月,某大型商业集团随机抽取所属的 家商业连锁店进行评估,将各连锁店按照评估成绩分成了 、 、 、 四个等级,绘制了如图尚不完整的统计图表.
|
评估成绩 (分) |
评定等级 |
频数 |
|
|
|
2 |
|
|
|
|
|
|
|
15 |
|
|
|
6 |
根据以上信息解答下列问题:
(1)求 的值;
(2)在扇形统计图中,求 等级所在扇形的圆心角的大小;(结果用度、分、秒表示)
(3)从评估成绩不少于80分的连锁店中任选2家介绍营销经验,求其中至少有一家是 等级的概率.
如图,反比例函数 的图象与一次函数 的图象交于 , 两点,点 的坐标为 ,点 的坐标为 .
(1)求反比例函数与一次函数的表达式;
(2)点 为 轴上一个动点,若 ,求点 的坐标.

一个盒子里有标号分别为1,2,3,4,5,6的六个小球,这些小球除标号数字外都相同.
(1)从盒中随机摸出一个小球,求摸到标号数字为奇数的小球的概率;
(2)甲、乙两人用这六个小球玩摸球游戏,规则是:甲从盒中随机摸出一个小球,记下标号数字后放回盒里,充分摇匀后,乙再从盒中随机摸出一个小球,并记下标号数字.若两次摸到小球的标号数字同为奇数或同为偶数,则判甲赢;若两次摸到小球的标号数字为一奇一偶,则判乙赢.请用列表法或画树状图的方法说明这个游戏对甲、乙两人是否公平.
某校进行期末体育达标测试,甲、乙两班的学生数相同,甲班有48人达标,乙班有45人达标,甲班的达标率比乙班高 ,求乙班的达标率.
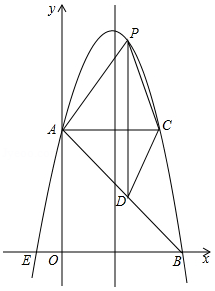
如图,在平面直角坐标系中,抛物线 的顶点坐标为 ,与 轴交于点 ,与 轴交于点 、 .
(1)求二次函数 的表达式;
(2)过点 作 平行于 轴,交抛物线于点 ,点 为抛物线上的一点(点 在 上方),作 平行于 轴交 于点 ,问当点 在何位置时,四边形 的面积最大?并求出最大面积;
(3)若点 在抛物线上,点 在其对称轴上,使得以 、 、 、 为顶点的四边形是平行四边形,且 为其一边,求点 、 的坐标.
某学校是乒乓球体育传统项目学校,为进一步推动该项目的开展,学校准备到体育用品店购买直拍球拍和横拍球拍若干副,并且每买一副球拍必须要买10个乒乓球,乒乓球的单价为2元 个,若购买20副直拍球拍和15副横拍球拍花费9000元;购买10副横拍球拍比购买5副直拍球拍多花费1600元.
(1)求两种球拍每副各多少元?
(2)若学校购买两种球拍共40副,且直拍球拍的数量不多于横拍球拍数量的3倍,请你给出一种费用最少的方案,并求出该方案所需费用.
如图,在平面直角坐标系中,正方形 的顶点 与坐标原点重合,点 的坐标为 ,点 在 轴的负半轴上,点 、 分别在边 、 上,且 , ,一次函数 的图象过点 和 ,反比例函数 的图象经过点 ,与 的交点为 .
(1)求反比例函数和一次函数的表达式;
(2)若点 在直线 上,且使 的面积与四边形 的面积相等,求点 的坐标.

随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的 型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少 ,求:
(1) 型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批 型车和新款 型车共60辆,且 型车的进货数量不超过 型车数量的两倍.已知 型车和 型车的进货价格分别为1500元和1800元,计划 型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?
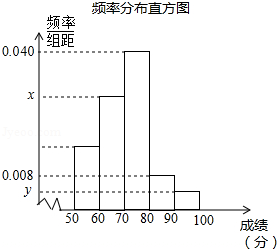
为参加学校的“我爱古诗词”知识竞赛,小王所在班级组织了一次古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计.以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图.
|
组别 |
分组 |
频数 |
频率 |
|
1 |
|
9 |
0.18 |
|
2 |
|
|
|
|
3 |
|
20 |
0.40 |
|
4 |
|
0.08 |
|
|
5 |
|
2 |
|
|
合计 |
请根据以上频率分布表和频率分布直方图,回答下列问题:
(1)求出 、 、 、 的值;
(2)老师说:“小王的测试成绩是全班同学成绩的中位数”,那么小王的测试成绩在什么范围内?
(3)若要从小明、小敏等五位成绩优秀的同学中随机选取两位参加竞赛,请用“列表法”或“树状图”求出小明、小敏同时被选中的概率.(注:五位同学请用 、 、 、 、 表示,其中小明为 ,小敏为 )
问题提出:如何将边长为 ,且 为整数)的正方形分割为一些 或 的矩形( 的矩形指边长分别为 , 的矩形)?
问题探究:我们先从简单的问题开始研究解决,再把复杂问题转化为已解决的问题.
探究一:
如图①,当 时,可将正方形分割为五个 的矩形.
如图②,当 时,可将正方形分割为六个 的矩形.
如图③,当 时,可将正方形分割为五个 的矩形和四个 的矩形
如图④,当 时,可将正方形分割为八个 的矩形和四个 的矩形
如图⑤,当 时,可将正方形分割为九个 的矩形和六个 的矩形

探究二:
当 ,11,12,13,14时,分别将正方形按下列方式分割:

所以,当 ,11,12,13,14时,均可将正方形分割为一个 的正方形、一个 的正方形和两个 的矩形.显然, 的正方形和 的矩形均可分割为 的矩形,而 的正方形是边长分别为5,6,7,8,9的正方形,用探究一的方法可分割为一些 或 的矩形.
探究三:
当 ,16,17,18,19时,分别将正方形按下列方式分割:

请按照上面的方法,分别画出边长为18,19的正方形分割示意图.
所以,当 ,16,17,18,19时,均可将正方形分割为一个 的正方形、一个 的正方形和两个 的矩形.显然, 的正方形和 的矩形均可分割为 的矩形,而 的正方形又是边长分别为5,6,7,8,9的正方形,用探究一的方法可分割为一些 或 的矩形.
问题解决:如何将边长为 ,且 为整数)的正方形分割为一些 或 的矩形?请按照上面的方法画出分割示意图,并加以说明.
实际应用:如何将边长为61的正方形分割为一些 或 的矩形?(只需按照探究三的方法画出分割示意图即可)
试题篮
()