初中数学计算题

某玩具厂生产一种玩具，本着控制固定成本，降价促销的原则，使生产的玩具能够全部售出．据市场调查，若按每个玩具280元销售时，每月可销售300个．若销售单价每降低1元，每月可多售出2个．据统计，每个玩具的固定成本 $Q$（元）与月产销量 $y$（个）满足如下关系：

月产销量 $y$（个）	$\dots$	160	200	240	300	$\dots$
每个玩具的固定成本 $Q$（元）	$\dots$	60	48	40	32	$\dots$

（1）写出月产销量 $y$（个）与销售单价 $x$（元）之间的函数关系式；

（2）求每个玩具的固定成本 $Q$（元）与月产销量 $y$（个）之间的函数关系式；

（3）若每个玩具的固定成本为30元，则它占销售单价的几分之几？

（4）若该厂这种玩具的月产销量不超过400个，则每个玩具的固定成本至少为多少元？销售单价最低为多少元？

如图，需在一面墙上绘制几个相同的抛物线型图案．按照图中的直角坐标系，最左边的抛物线可以用 $y=a{x}^2+\mathit{bx}(a\ne 0)$表示．已知抛物线上 $B$， $C$两点到地面的距离均为 $\frac{3}{4}m$，到墙边 $\mathit{OA}$的距离分别为 $\frac{1}{2}m$， $\frac{3}{2}m$．

（1）求该拋物线的函数关系式，并求图案最高点到地面的距离；

（2）若该墙的长度为 $10m$，则最多可以连续绘制几个这样的拋物线型图案？

甲、乙两名队员参加射击训练，成绩分别被制成下列两个统计图：

根据以上信息，整理分析数据如下：

	平均成绩 $/$环	中位数 $/$环	众数 $/$环	方差
甲	$a$	7	7	1.2
乙	7	$b$	8	$c$

（1）写出表格中 $a$， $b$， $c$的值；

（2）分别运用表中的四个统计量，简要分析这两名队员的射击训练成绩．若选派其中一名参赛，你认为应选哪名队员？

如图， $\mathit{AB}$是长为 $10m$，倾斜角为 $37°$的自动扶梯，平台 $\mathit{BD}$与大楼 $\mathit{CE}$垂直，且与扶梯 $\mathit{AB}$的长度相等，在 $B$处测得大楼顶部 $C$的仰角为 $65°$，求大楼 $\mathit{CE}$的高度（结果保留整数）．

（参考数据： $\sin 37°\approx \frac{3}{5}$， $\tan 37°\approx \frac{3}{4}$， $\sin 65°\approx \frac{9}{10}$， $\tan 65°\approx \frac{15}{7})$

（1）化简： $\frac{x+1}{x-1}-\frac{4x}{x^2-1}$

（2）解不等式组 $\left\{\begin{array}{c}\frac{x+1}{2}⩽1\\ 5x-8<9x\end{array}\right.$，并写出它的整数解．

现代互联网技术的广泛应用，催生了快递行业的高速发展．小明计划给朋友快递一部分物品，经了解有甲、乙两家快递公司比较合适．甲公司表示：快递物品不超过1千克的，按每千克22元收费；超过1千克，超过的部分按每千克15元收费．乙公司表示：按每千克16元收费，另加包装费3元．设小明快递物品 $x$千克．

（1）请分别写出甲、乙两家快递公司快递该物品的费用 $y$（元）与 $x$（千克）之间的函数关系式；

（2）小明选择哪家快递公司更省钱？

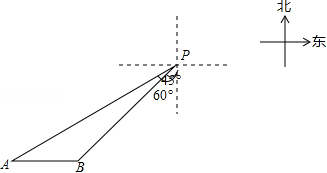
一艘轮船位于灯塔 $P$南偏西 $60°$方向，距离灯塔20海里的 $A$处，它向东航行多少海里到达灯塔 $P$南偏西 $45°$方向上的 $B$处（参考数据： $\sqrt{3}\approx 1.732$，结果精确到 $0.1)$？

计算： $|-3|+\sqrt{3}\tan 30°-\sqrt{12}-{(2016-\pi )}^0$．

如图，在直角坐标系中，直线 $y=-\frac{1}{2}x$与反比例函数 $y=\frac{k}{x}$的图象交于关于原点对称的 $A$， $B$两点，已知 $A$点的纵坐标是3．

（1）求反比例函数的表达式；

（2）将直线 $y=-\frac{1}{2}x$向上平移后与反比例函数在第二象限内交于点 $C$，如果 $\mathit{\Delta ABC}$的面积为48，求平移后的直线的函数表达式．

为加快城市群的建设与发展，在 $A$， $B$两城市间新建一条城际铁路，建成后，铁路运行里程由现在的 $120\mathit{km}$缩短至 $114\mathit{km}$，城际铁路的设计平均时速要比现行的平均时速快 $110\mathit{km}$，运行时间仅是现行时间的 $\frac{2}{5}$，求建成后的城际铁路在 $A$， $B$两地的运行时间．

为了让书籍开拓学生的视野，陶冶学生的情操，向阳中学开展了“五个一”课外阅读活动，为了解全校学生课外阅读情况，抽样调查了50名学生平均每天课外阅读时间（单位： $\mathit{min}$），将抽查得到的数据分成5组，下面是尚未完成的频数、频率分布表：

组别	分组	频数（人数）	频率
1	$10⩽t<30$		0.16
2	$30⩽t<50$	20
3	$50⩽t<70$		0.28
4	$70⩽t<90$	6
5	$90⩽t<110$

（1）将表中空格处的数据补全，完成上面的频数、频率分布表；

（2）请在给出的平面直角坐标系中画出相应的频数直方图；

（3）如果该校有1500名学生，请你估计该校共有多少名学生平均每天阅读时间不少于 $50\mathit{min}$？

如图，在平面直角坐标系中，已知 $\mathit{\Delta ABC}$的三个顶点的坐标分别为 $A(-3,5)$， $B(-2,1)$， $C(-1,3)$．

（1）若 $\mathit{\Delta ABC}$经过平移后得到△ $A_1{B}_1{C}_1$，已知点 $C_1$的坐标为 $(4,0)$，写出顶点 $A_1$， $B_1$的坐标；

（2）若 $\mathit{\Delta ABC}$和△ $A_2{B}_2{C}_2$关于原点 $O$成中心对称图形，写出△ $A_2{B}_2{C}_2$的各顶点的坐标；

（3）将 $\mathit{\Delta ABC}$绕着点 $O$按顺时针方向旋转 $90°$得到△ $A_3{B}_3{C}_3$，写出△ $A_3{B}_3{C}_3$的各顶点的坐标．

计算： $(\frac{x+8}{x^2-4}-\frac{2}{x-2})÷\frac{x-4}{x^2-4x+4}$．

为迎接“国家卫生城市”复检，某市环卫局准备购买 $A$、 $B$两种型号的垃圾箱，通过市场调研得知：购买3个 $A$型垃圾箱和2个 $B$型垃圾箱共需540元；购买2个 $A$型垃圾箱比购买3个 $B$型垃圾箱少用160元．

（1）每个 $A$型垃圾箱和 $B$型垃圾箱各多少元？

（2）现需要购买 $A$， $B$两种型号的垃圾箱共300个，分别由甲、乙两人进行安装，要求在12天内完成（两人同时进行安装）．已知甲负责 $A$型垃圾箱的安装，每天可以安装15个，乙负责 $B$型垃圾箱的安装，每天可以安装20个，生产厂家表示若购买 $A$型垃圾箱不少于150个时，该型号的产品可以打九折；若购买 $B$型垃圾箱超过150个时，该型号的产品可以打八折，若既能在规定时间内完成任务，费用又最低，应购买 $A$型和 $B$型垃圾箱各多少个？最低费用是多少元？

某体育场看台的坡面 $\mathit{AB}$与地面的夹角是 $37°$，看台最高点 $B$到地面的垂直距离 $\mathit{BC}$为3.6米，看台正前方有一垂直于地面的旗杆 $\mathit{DE}$，在 $B$点用测角仪测得旗杆的最高点 $E$的仰角为 $33°$，已知测角仪 $\mathit{BF}$的高度为1.6米，看台最低点 $A$与旗杆底端 $D$之间的距离为16米（ $C$， $A$， $D$在同一条直线上）．

（1）求看台最低点 $A$到最高点 $B$的坡面距离；

（2）一面红旗挂在旗杆上，固定红旗的上下两个挂钩 $G$、 $H$之间的距离为1.2米，下端挂钩 $H$与地面的距离为1米，要求用30秒的时间将红旗升到旗杆的顶端，求红旗升起的平均速度（计算结果保留两位小数） $(\sin 37°\approx 0.6$， $\cos 37°\approx 0.8$， $\tan 37°\approx 0.75$， $\sin 33°\approx 0.54$， $\cos 33°\approx 0.84$， $\tan 33°\approx 0.65)$