初中数学解答题

如图，在平行四边形ABCD中，若AB=6，AD=10，∠ABC的平分线交AD于点E，交CD的延长线于点F，求DF的长．

先化简，再求值：，其中a，b满足=0．

（1）计算：－tan30°
（2）解方程：；
（3）解不等式组，并把解集在数轴上表示出来．

如图，矩形ABCD中，AB=8，AD=6，点E、F分别在边CD、AB上．

（1）若DE=BF，求证：四边形AFCE是平行四边形；
（2）若四边形AFCE是菱形，求菱形AFCE的周长．

已知抛物线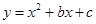与x轴交于A，B两点，与y轴交于点C，O是坐标原点，点A的坐标是（﹣1，0），点C的坐标是（0，﹣3）．

（1）求抛物线的函数表达式；
（2）求直线BC的函数表达式和∠ABC的度数；
（3）P为线段BC上一点，连接AC，AP，若∠ACB=∠PAB，求点P的坐标．

图（1）是一个蒙古包的照片，这个蒙古包可以近似看成是圆锥和圆柱组成的几何体，如图（2）所示．

（1）请画出这个几何体的俯视图；
（2）图（3）是这个几何体的正面示意图，已知蒙古包的顶部离地面的高度EO₁=6米，圆柱部分的高OO₁=4米，底面圆的直径BC=8米，求∠EAO的度数（结果精确到0.1°）．

为开展“争当书香少年”活动，小石对本校部分同学进行“最喜欢的图书类别”的问卷调查，结果统计后，绘制了如下两幅不完整的统计图：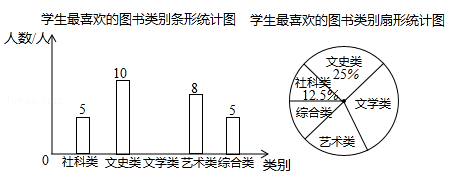

根据以上统计图提供的信息，回答下列问题：
（1）此次被调查的学生共人；
（2）补全条形统计图；
（3）扇形统计图中，艺术类部分所对应的圆心角为度；
（4）若该校有1200名学生，估计全校最喜欢“文史类”图书的学生有人．

如图，四边形ABCD为矩形，E为BC边中点，连接AE，以AD为直径的⊙O交AE于点F，连接CF．

（1）求证：CF与⊙O相切；
（2）若AD=2，F为AE的中点，求AB的长．

解分式方程：．

化简：．

如图，已知Rt△ABC中，∠C=90°，AC=8，BC=6，点P以每秒1个单位的速度从A向C运动，同时点Q以每秒2个单位的速度从A→B→C方向运动，它们到C点后都停止运动，设点P，Q运动的时间为t秒．

（1）在运动过程中，求P，Q两点间距离的最大值；
（2）经过t秒的运动，求△ABC被直线PQ扫过的面积S与时间t的函数关系式；
（3）P，Q两点在运动过程中，是否存在时间t，使得△PQC为等腰三角形？若存在，求出此时的t值；若不存在，请说明理由（≈2．24，结果保留一位小数）

已知：如图，在△ABC中，DE、DF是△ABC的中位线，连接EF、AD，其交点为O．求证：

（1）△CDE≌△DBF；
（2）OA=OD．

如图，抛物线 $y=x2+bx+c$与 $x$轴交于 $A（﹣1，0），B（3，0）$两点，顶点 $M$关于 $x$轴的对称点是 $M\prime$．

（1）求抛物线的解析式；
（2）若直线 $AM\prime$与此抛物线的另一个交点为 $C$，求 $△CAB$的面积；
（3）是否存在过 $A，B$两点的抛物线，其顶点 $P$关于 $x$轴的对称点为 $Q$，使得四边形 $APBQ$为正方形？若存在，求出此抛物线的解析式；若不存在，请说明理由．

如图，折叠矩形OABC的一边BC，使点C落在OA边的点D处，已知折痕BE=5，且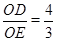，以O为原点，OA所在的直线为x轴建立如图所示的平面直角坐标系，抛物线l：y=－+c经过点E，且与AB边相交于点F．

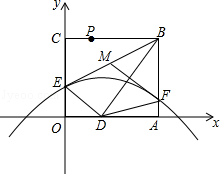
（1）求证：△ABD∽△ODE；
（2）若M是BE的中点，连接MF，求证：MF⊥BD；
（3）P是线段BC上一点，点Q在抛物线l上，且始终满足PD⊥DQ，在点P运动过程中，能否使得PD=DQ？若能，求出所有符合条件的Q点坐标；若不能，请说明理由．

阅读材料：善于思考的小军在解方程组时，采用了一种“整体代换”的解法：
解：将方程②变形：4x+10y+y="5" 即2（2x+5y）+y=5③
把方程①带入③得：2×3+y=5，∴y=﹣1
把y=﹣1代入①得x=4，∴方程组的解为．
请你解决以下问题：
（1）模仿小军的“整体代换”法解方程组
（2）已知x，y满足方程组．
（i）求的值；
（ii）求的值．