初中数学解答题

如图，抛物线y=与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C．

（1）求点A、B的坐标；
（2）设D为已知抛物线的对称轴上的任意一点，当△ACD的面积等于△ACB的面积时，求点D的坐标；
（3）若直线l过点E（4，0），M为直线l上的动点，当以A、B、M为顶点所作的直角三角形有且只有三个时，求直线l的解析式．

在矩形ABCD中，点P在AD上，AB=2，AP=1．将直角尺的顶点放在P处，直角尺的两边分别交AB，BC于点E，F，连接EF（如图①）．

（1）当点E与点B重合时，点F恰好与点C重合（如图②），求PC的长；
（2）探究：将直尺从图②中的位置开始，绕点P顺时针旋转，当点E和点A重合时停止．在这个过程中，请你观察、猜想，并解答：
①tan∠PEF的值是否发生变化？请说明理由；
②直接写出从开始到停止，线段EF的中点经过的路线长．

如图，在方格纸上建立平面直角坐标系，每个小正方形的边长为1．

（1）画出△AOB关于x轴对称的△A₁OB₁．
（2）画出将△AOB绕点O顺时针旋转90°的△A₂OB₂，并判断△A₁OB₁和△A₂OB₂在位置上有何关系？若成中心对称，请直接写出对称中心坐标；如成轴对称，请直接写出对称轴的函数关系式．
（3）若将△AOB绕点O旋转360°，试求出线段AB扫过的面积．

二次函数y=x²-2mx+3（m＞）的图象与x轴交于点A（a，0）和点B（a+n，0）（n＞0且n为整数），与y轴交于C点．
（1）若a=1，①求二次函数关系式；②求△ABC的面积；
（2）求证：a=m-；
（3）线段AB（包括A、B）上有且只有三个点的横坐标是整数，求a的值．

如图1，某超市从底楼到二楼有一自动扶梯，图2是侧面示意图．已知自动扶梯AB的长度是12．5米，MN是二楼楼顶，MN∥PQ，C是MN上处在自动扶梯顶端B点正上方的一点，BC⊥MN，在自动扶梯底端A处测得C点的仰角∠CAQ为45°，坡角∠BAQ为37°，求二楼的层高BC（精确到0．1米）．（参考数据：sin37°≈0．60，cos37°≈0．80，tan37°≈0．75 ）

如图，在矩形ABCD中，AD=8，AB=6，点M是BC的中点，点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动，到达点B后立刻以原速度沿BM返回；点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动，在点P，Q的运动过程中，以PQ为边作正方形PQEF，使它与矩形ABCD在BC的同侧，点P，Q同时出发，当点P返回点M时停止运动，点Q也随之停止，设点P，Q运动的时间是t秒（t＞0）

（1）用含t的代数式表示线段BQ的长；
（2）设正方形PQEF与矩形ABCD重叠部分的面积为S，求S与t之间的函数关系式；
（3）连接AC，当正方形PQEF与△ADC重叠部分为三角形时，直接写出t的取值范围．

某企业生产的一批产品上市后30天内全部售完，调查发现，国内市场的日销售量为y₁（吨）与时间t（t为整数，单位：天）的关系如图1所示的抛物线的一部分，而国外市场的日销售量y₂（吨）与时间t，t为整数，单位：天）的关系如图2所示．

（1）求y₁与时间t的函数关系式及自变量t的取值范围，并写出y₂与t的函数关系式及自变量t的取值范围；
（2）设国内、国外市场的日销售总量为y吨，直接写出y与时间t的函数关系式，当销售第几天时，国内、外市场的日销售总量最早达到75吨？
（3）判断上市第几天国内、国外市场的日销售总量y最大，并求出此时的最大值．

在△ABC中，BA=BC，∠BAC=α，M是AC的中点，P是线段BM上的动点，将线段PA绕点P顺时针旋转2α转得到线段PQ．

（1）若α=60°且点P与点M重合（如图1），线段CQ的延长线交射线BM于点D．求∠CDB的度数；
（2）在图2中，点P不与点B，M重合，线段CQ的延长线于射线BM交于点D，求∠CDB的大小（用含α的代数式表示）；
（3）对于适当大小的α，当点P在线段BM上运动到某一位置（不与点B，M重合）时，能使得线段CQ的延长线与射线BM交于点D，且PQ=QD，请求α的取值范围．

某小区超市一段时间每天订购80个面包进行销售，每售出1个面包获利润0．5元，未售出的每个亏损0．3元．（1）若今后每天售出的面包个数用x（0＜x≤80）表示，每天销售面包的利润用y（元）表示，写出y与x的函数关系式；
（2）小明连续m天对该超市的面包销量进行统计，并制成了频数分别直方图（每个组距包含左边的数，但不包含右边的数）和扇形统计图，如图1、图2所示，请结合两图提供的信息，解答下列问题：
①m的值为 ；
②求在m天内日销售利润少于32元的天数；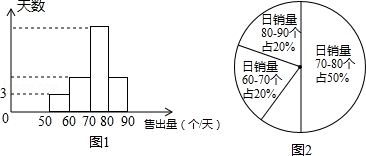

（3）如图（2）中m天内日销售面包个数在70≤x＜80这个组内的销售情况如表：

销售量/个	70	72	73	75	78	79
天数	1	2	3	4	3	2

请计算该组内平均每天销售面包的个数．

已知一元二次方程ax²+2x-=0有唯一的解，求的值．

抛物线与x轴交于A，B两点，（点B在点A的左侧）且A，B两点的坐标分别为（-2，0）、（8，0），与y轴交于点C，连接BC，以BC为一边，点O为对称中心作菱形BDEC，点P是x轴上的一个动点，设点P的坐标为（m，0），过点P作x轴的垂线L交抛物线于点Q，交BD于点M．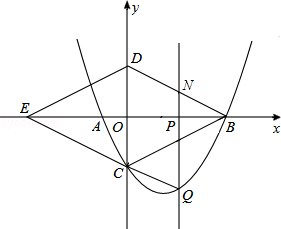

（1）求抛物线的解析式；
（2）当点P在线段OB上运动时，试探究m为何值时，四边形CQMD是平行四边形？
（3）在（2）的结论下，试问抛物线上是否存在点N（不同于点Q），使三角形BCN的面积等于三角形BCQ的面积？若存在，请求出点N的坐标；若不存在，请说明理由．

在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角（两边足够长），用28m长的篱笆围成一个矩形花园ABCD（篱笆只围AB，BC两边），设AB=xm．

（1）若花园的面积为192m²，求x的值；
（2）若在P处有一棵树与墙CD，AD的距离分别是15m和6m，要将这棵树围在花园内（含边界，不考虑树的粗细），求花园面积S的最大值．

如图，将平行四边形ABCD纸片沿EF折叠，使点C与点A重合，点D落在点G处，

（1）求证：四边形AECF是菱形；
（2）连接AC，若平行四边形ABCD的面积为8，，求AC•EF的值．

如图，已知反比例函数y=（x＞0，k是常数）的图象经过点A（1，4），点B（m，n），其中m＞1，AM⊥x轴，垂足为M，BN⊥y轴，垂足为N，AM与BN的交点为C．

（1）写出反比例函数解析式；
（2）求证：△ACB∽△NOM；
（3）若△ACB与△NOM的相似比为2，求出B点的坐标及AB所在直线的解析式．

已知：如图，在▱ABCD中，O为对角线BD的中点，过点O的直线EF分别交AD，BC于E，F两点，连结BE，DF．

（1）求证：△DOE≌△BOF；
（2）当∠DOE等于多少度时，四边形BFDE为菱形？请说明理由．