如图,在 中, , , ,以 为直径作 交 于点 .
(1)求线段 的长度;
(2)点 是线段 上的一点,试问:当点 在什么位置时,直线 与 相切?请说明理由.

现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整)
|
步数 |
频数 |
频率 |
|
|
8 |
|
|
|
15 |
0.3 |
|
|
12 |
|
|
|
|
0.2 |
|
|
3 |
0.06 |
|
|
|
0.04 |
请根据以上信息,解答下列问题:
(1)写出 , , , 的值并补全频数分布直方图;
(2)本市约有37800名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步)的两名教师与大家分享心得,求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.

如图,一次函数 、 为常数, 的图象与 轴、 轴分别交于 、 两点,且与反比例函数 为常数,且 的图象在第二象限交于点 . 轴,垂足为 ,若 .
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为 ,求 的面积;
(3)直接写出不等式 的解集.

如图,在 的方格纸中, 的三个顶点都在格点上.
(1)在图1中,画出一个与 成中心对称的格点三角形;
(2)在图2中,画出一个与 成轴对称且与 有公共边的格点三角形;
(3)在图3中,画出
绕着点
按顺时针方向旋转
后的三角形.
【问题解决】
一节数学课上,老师提出了这样一个问题:如图1,点 是正方形 内一点, , , .你能求出 的度数吗?
小明通过观察、分析、思考,形成了如下思路:
思路一:将 绕点 逆时针旋转 ,得到△ ,连接 ,求出 的度数;
思路二:将 绕点 顺时针旋转 ,得到△ ,连接 ,求出 的度数.
请参考小明的思路,任选一种写出完整的解答过程.
【类比探究】
如图2,若点 是正方形 外一点, , , ,求 的度数.

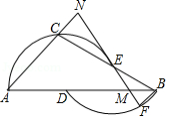
如图,已知 , 分别为 的边 , 上两点,点 , , 在 上,点 , 在 上. 为 上一点,连接 并延长交 的延长线于点 ,交 于点 .
(1)若 为 ,请将 用含 的代数式表示;
(2)若 ,请说明当 为多少度时,直线 为 的切线;
(3)在(2)的条件下,若 ,求 的值.
为提高市民的环保意识,倡导“节能减排,绿色出行”,某市计划在城区投放一批“共享单车”.这批单车分为 , 两种不同款型,其中 型车单价400元, 型车单价320元.
(1)今年年初,“共享单车”试点投放在某市中心城区正式启动.投放 , 两种款型的单车共100辆,总价值36800元.试问本次试点投放的 型车与 型车各多少辆?
(2)试点投放活动得到了广大市民的认可,该市决定将此项公益活动在整个城区全面铺开.按照试点投放中 , 两车型的数量比进行投放,且投资总价值不低于184万元.请问城区10万人口平均每100人至少享有 型车与 型车各多少辆?
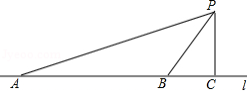
汽车超速行驶是交通安全的重大隐患,为了有效降低交通事故的发生,许多道路在事故易发路段设置了区间测速.如图,学校附近有一条笔直的公路 ,其间设有区间测速,所有车辆限速40千米 小时.数学实践活动小组设计了如下活动:在 上确定 , 两点,并在 路段进行区间测速.在 外取一点 ,作 ,垂足为点 .测得 米, , .上午9时测得一汽车从点 到点 用时6秒,请你用所学的数学知识说明该车是否超速.(参考数据: , , , , ,
随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.

如图1,在 中, 于点 , 的垂直平分线交 于点 ,交 于点 , , , .
(1)如图2,作 于点 ,交 于点 ,将 沿 方向平移,得到△ ,连接 .
①求四边形 的面积;
②直线 上有一动点 ,求 周长的最小值.
(2)如图3,延长 交 于点 ,过点 作 ,过 边上的动点 作 ,并与 交于点 ,将 沿直线 翻折,使点 的对应点 恰好落在直线 上,求线段 的长.

为落实“绿水青山就是金山银山”的发展理念,某市政部门招标一工程队负责在山脚下修建一座水库的土方施工任务.该工程队有 , 两种型号的挖掘机,已知3台 型和5台 型挖掘机同时施工一小时挖土165立方米;4台 型和7台 型挖掘机同时施工一小时挖土225立方米.每台 型挖掘机一小时的施工费用为300元,每台 型挖掘机一小时的施工费用为180元.
(1)分别求每台 型, 型挖掘机一小时挖土多少立方米?
(2)若不同数量的 型和 型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元,问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元?
为进一步提高全民“节约用水”意识,某学校组织学生进行家庭月用水量情况调查活动,小莹随机抽查了所住小区 户家庭的月用水量,绘制了下面不完整的统计图.

(1)求 并补全条形统计图;
(2)求这 户家庭的月平均用水量;并估计小莹所住小区420户家庭中月用水量低于月平均用水量的家庭户数;
(3)从月用水量为 和 的家庭中任选两户进行用水情况问卷调查,求选出的两户中月用水量为 和 恰好各有一户家庭的概率.
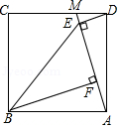
如图,点 是正方形 边 上一点,连接 ,作 于点 , 于点 ,连接 .
(1)求证: ;
(2)已知 ,四边形 的面积为24,求 的正弦值.
试题篮
()