初中数学解答题

如图，直线 $y_1=\mathit{mx}+n(m\ne 0)$与双曲线 $y_2=\frac{k}{x}(k\ne 0)$相交于 $A(-1,2)$和 $B(2,b)$两点，与 $y$轴交于点 $C$，与 $x$轴交于点 $D$．

（1）求 $m$， $n$的值；

（2）在 $y$轴上是否存在一点 $P$，使 $\mathit{\Delta BCP}$与 $\mathit{\Delta OCD}$相似？若存在求出点 $P$的坐标；若不存在，请说明理由．

关于三角函数有如下公式： $\sin (\alpha +\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta$， $\sin (\alpha -\beta )=\sin \alpha \cos \beta -\cos \alpha \sin \beta$

$\cos (\alpha +\beta )=\cos \alpha \cos \beta -\sin \alpha \sin \beta$， $\cos (\alpha -\beta )=\cos \alpha \cos \beta +\sin \alpha \sin \beta$

$\tan (\alpha +\beta )=\frac{\tan \alpha +\tan \beta }{1-\tan \alpha \tan \beta }(1-\tan \alpha \tan \beta \ne 0)$

$\tan (\alpha -\beta )=\frac{\tan \alpha -\tan \beta }{1+\tan \alpha \tan \beta }(1+\tan \alpha \tan \beta \ne 0)$

利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值．

如： $\tan 105°=\tan (45°+60°)=\frac{\tan 45°+\tan 60°}{1-\tan 45°\tan 60°}=\frac{1+\sqrt{3}}{1-\sqrt{3}}=-2-\sqrt{3}$

根据上面的知识，你可以选择适当的公式解决下面问题：

如图，两座建筑物 $\mathit{AB}$和 $\mathit{DC}$的水平距离 $\mathit{BC}$为24米，从点 $A$测得点 $D$的俯角 $\alpha =15°$，测得点 $C$的俯角 $\beta =75°$，求建筑物 $\mathit{CD}$的高度．

2017年遂宁市吹响了全国文明城市创建决胜“集结号”．为了加快创建步伐，某运输公司承担了某标段的土方运输任务，公司已派出大小两种型号的渣土运输车运输土方．已知一辆大型渣土运输车和一辆小型渣土运输车每次共运15吨；3辆大型渣土运输车和8辆小型渣土运输车每次共运70吨．

（1）一辆大型渣土运输车和一辆小型渣土运输车每次各运土方多少吨？

（2）该渣土运输公司决定派出大小两种型号渣土运输车共20辆参与运输土方，若每次运输土方总量不小于148吨，且小型渣土运输车至少派出7辆，问该渣土运输公司有几种派出方案？

（3）在（2）的条件下，已知一辆大型渣土运输车运输花费500元 $/$次，一辆小型渣土运输车运输花费300元 $/$次，为了节约开支，该公司应选择哪种方案划算？

在一次社会调查活动中，小李收集到某“健步走运动”团队20名成员一天行走的步数，记录如下：

5640	6430	6520	6798	7325
8430	8215	7453	7446	6754
7638	6834	7326	6830	8648
8753	9450	9865	7290	7850

对这20个数据按组距1000进行分组，并统计整理，绘制了如下不完整的统计图表，步数分布统计图．

组别	步数分组	频数
$A$	$5500⩽x<6500$	$m$
$B$	$6500⩽x<7500$	10
$C$	$7500⩽x<8500$	4
$D$	$8500⩽x<9500$	$n$
$E$	$9500⩽x<10500$	1

根据以上信息解答下列问题：

（1）填空： $m=$　　， $n=$　　；

（2）请补全条形统计图；

（3）这20名“健步走运动”团队成员一天行走的步数的中位数落在　　组；

（4）若该团队共有200人，请估计其中一天行走步数少于8500步的人数．

如图，在平行四边形 $\mathit{ABCD}$中， $\mathit{BD}$为对角线， $\mathit{AE}\perp \mathit{BD}$， $\mathit{CF}\perp \mathit{BD}$，垂足分别为 $E$、 $F$，连接 $\mathit{AF}$、 $\mathit{CE}$．

求证： $\mathit{AF}=\mathit{CE}$．

如图1，在平面直角坐标系中，直线 $\mathit{MN}$分别与 $x$轴、 $y$轴交于点 $M(6,0)$， $N(0$， $2\sqrt{3})$，等边 $\mathit{\Delta ABC}$的顶点 $B$与原点 $O$重合， $\mathit{BC}$边落在 $x$轴正半轴上，点 $A$恰好落在线段 $\mathit{MN}$上，将等边 $\mathit{\Delta ABC}$从图1的位置沿 $x$轴正方向以每秒1个单位长度的速度平移，边 $\mathit{AB}$， $\mathit{AC}$分别与线段 $\mathit{MN}$交于点 $E$， $F$（如图2所示），设 $\mathit{\Delta ABC}$平移的时间为 $t\left(s\right)$．

（1）等边 $\mathit{\Delta ABC}$的边长为　　；

（2）在运动过程中，当 $t=$　　时， $\mathit{MN}$垂直平分 $\mathit{AB}$；

（3）若在 $\mathit{\Delta ABC}$开始平移的同时．点 $P$从 $\mathit{\Delta ABC}$的顶点 $B$出发．以每秒2个单位长度的速度沿折线 $\mathit{BA}-\mathit{AC}$运动．当点 $P$运动到 $C$时即停止运动． $\mathit{\Delta ABC}$也随之停止平移．

①当点 $P$在线段 $\mathit{BA}$上运动时，若 $\mathit{\Delta PEF}$与 $\mathit{\Delta MNO}$相似．求 $t$的值；

②当点 $P$在线段 $\mathit{AC}$上运动时，设 $S_{\mathit{\Delta PEF}}=S$，求 $S$与 $t$的函数关系式，并求出 $S$的最大值及此时点 $P$的坐标．

如图， $\mathit{\Delta ABC}$中，以 $\mathit{BC}$为直径的 $\odot O$交 $\mathit{AB}$于点 $D$， $\mathit{AE}$平分 $\angle \mathit{BAC}$交 $\mathit{BC}$于点 $E$，交 $\mathit{CD}$于点 $F$．且 $\mathit{CE}=\mathit{CF}$．

（1）求证：直线 $\mathit{CA}$是 $\odot O$的切线；

（2）若 $\mathit{BD}=\frac{4}{3}\mathit{DC}$，求 $\frac{\mathit{DF}}{\mathit{CF}}$的值．

如图，在平面直角坐标系中，坐标原点 $O$是菱形 $\mathit{ABCD}$的对称中心．边 $\mathit{AB}$与 $x$轴平行，点 $B(1,-2)$，反比例函数 $y=\frac{k}{x}(k\ne 0)$的图象经过 $A$， $C$两点．

（1）求点 $C$的坐标及反比例函数的解析式．

（2）直线 $\mathit{BC}$与反比例函数图象的另一交点为 $E$，求以 $O$， $C$， $E$为顶点的三角形的面积．

攀枝花芒果由于品质高、口感好而闻名全国，通过优质快捷的网络销售渠道，小明的妈妈先购买了2箱 $A$品种芒果和3箱 $B$品种芒果，共花费450元；后又购买了1箱 $A$品种芒果和2箱 $B$品种芒果，共花费275元（每次两种芒果的售价都不变）．

（1）问 $A$品种芒果和 $B$品种芒果的售价分别是每箱多少元？

（2）现要购买两种芒果共18箱，要求 $B$品种芒果的数量不少于 $A$品种芒果数量的2倍，但不超过 $A$品种芒果数量的4倍，请你设计购买方案，并写出所需费用最低的购买方案．

如图，在平行四边形 $\mathit{ABCD}$中， $\mathit{AE}\perp \mathit{BC}$， $\mathit{CF}\perp \mathit{AD}$，垂足分别为 $E$， $F$， $\mathit{AE}$， $\mathit{CF}$分别与 $\mathit{BD}$交于点 $G$和 $H$，且 $\mathit{AB}=2\sqrt{5}$．

（1）若 $\tan \angle \mathit{ABE}=2$，求 $\mathit{CF}$的长；

（2）求证： $\mathit{BG}=\mathit{DH}$．

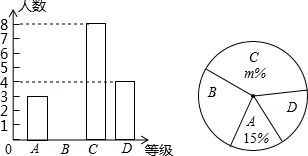
中华文明，源远流长；中华汉字，寓意深广．为了传承中华民族优秀传统文化，我市某中学举行“汉字听写”比赛，赛后整理参赛学生的成绩，将学生的成绩分为 $A$， $B$， $C$， $D$四个等级，并将结果绘制成如图所示的条形统计图和扇形统计图，但均不完整．

请你根据统计图解答下列问题：

（1）参加比赛的学生共有　　名；

（2）在扇形统计图中， $m$的值为　　，表示“ $D$等级”的扇形的圆心角为　　度；

（3）组委会决定从本次比赛获得 $A$等级的学生中，选出2名去参加全市中学生“汉字听写”大赛．已知 $A$等级学生中男生有1名，请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率．

如图，在中，直径垂直于不过圆心的弦，垂足为点，连接，点在上，且

（1）求证：；

（2）过点作的切线交的延长线于点，试判断与是否相等，并说明理由；

（3）设半径为4，点为中点，点在上，求线段的最小值．

已知、两点是一次函数和反比例函数图象的两个交点．

（1）求一次函数和反比例函数的解析式；

（2）求的面积；

（3）观察图象，直接写出不等式的解集．

如图，某人为了测量小山顶上的塔的高，他在山下的点处测得塔尖点的仰角为，再沿方向前进到达山脚点，测得塔尖点的仰角为，塔底点的仰角为，求塔的高度．（结果保留根号）

小明随机调查了若干市民租用共享单车的骑车时间（单位：分），将获得的数据分成四组，绘制了如下统计图，，，，根据图中信息，解答下列问题：

（1）这项被调查的总人数是多少人？

（2）试求表示组的扇形统计图的圆心角的度数，补全条形统计图；

（3）如果小明想从组的甲、乙、丙、丁四人中随机选择两人了解平时租用共享单车情况，请用列表或画树状图的方法求出恰好选中甲的概率．