从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在 中, 为角平分线, , ,求证: 为 的完美分割线.
(2)在 中, , 是 的完美分割线,且 为等腰三角形,求 的度数.
(3)如图2, 中, , , 是 的完美分割线,且 是以 为底边的等腰三角形,求完美分割线 的长.

某商场销售 , 两种品牌的教学设备,这两种教学设备的进价和售价如表所示
|
|
|
|
|
进价(万元 套) |
1.5 |
1.2 |
|
售价(万元 套) |
1.65 |
1.4 |
该商场计划购进两种教学设备若干套,共需66万元,全部销售后可获毛利润9万元.
(1)该商场计划购进 , 两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少 种设备的购进数量,增加 种设备的购进数量,已知 种设备增加的数量是 种设备减少的数量的1.5倍.若用于购进这两种教学设备的总资金不超过69万元,问 种设备购进数量至多减少多少套?
如图,已知 的直径 ,弦 , 的平分线交 于点 ,过点 作 交 的延长线于点 .
(1)求证: 是 的切线.
(2)求 的长.

如图,已知抛物线 与 轴交于 , 两点,与 轴交于点 ,点 的坐标为
(1)求 的值及抛物线的顶点坐标.
(2)点 是抛物线对称轴 上的一个动点,当 的值最小时,求点 的坐标.

为深化义务教育课程改革,某校积极开展拓展性课程建设,计划开设艺术、体育、劳技、文学等多个类别的拓展性课程,要求每一位学生都自主选择一个类别的拓展性课程.为了了解学生选择拓展性课程的情况,随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图(部分信息未给出)

根据统计图中的信息,解答下列问题:
(1)求本次被调查的学生人数.
(2)将条形统计图补充完整.
(3)若该校共有1600名学生,请估计全校选择体育类的学生人数.
下列 网格图都是由9个相同的小正方形组成,每个网格图中有3个小正方形已涂上阴影,请在余下的6个空白小正方形中,按下列要求涂上阴影:

(1)选取1个涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形.
(2)选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形.
(3)选取2个涂上阴影,使5个阴影小正方形组成一个轴对称图形.
(请将三个小题依次作答在图1、图2、图3中,均只需画出符合条件的一种情形)
如图1,地面 上两根等长立柱 , 之间悬挂一根近似成抛物线 的绳子.

(1)求绳子最低点离地面的距离;
(2)因实际需要,在离 为3米的位置处用一根立柱 撑起绳子(如图 ,使左边抛物线 的最低点距 为1米,离地面1.8米,求 的长;
(3)将立柱 的长度提升为3米,通过调整 的位置,使抛物线 对应函数的二次项系数始终为 ,设 离 的距离为 ,抛物线 的顶点离地面距离为 ,当 时,求 的取值范围.
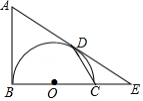
如图, 是以 为直径的半圆 的切线, 为半圆上一点, , , 的延长线相交于点 .
(1)求证: 是半圆 的切线;
(2)连接 ,求证: ;
(3)若 , ,求 的长.
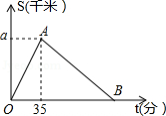
2016年3月27日“丽水半程马拉松竞赛”在莲都举行,某运动员从起点万地广场西门出发,途经紫金大桥,沿比赛路线跑回终点万地广场西门.设该运动员离开起点的路程 (千米)与跑步时间 (分钟)之间的函数关系如图所示,其中从起点到紫金大桥的平均速度是0.3千米 分,用时35分钟,根据图象提供的信息,解答下列问题:
(1)求图中 的值;
(2)组委会在距离起点2.1千米处设立一个拍摄点 ,该运动员从第一次经过 点到第二次经过 点所用的时间为68分钟.
①求 所在直线的函数解析式;
②该运动员跑完赛程用时多少分钟?

为了帮助九年级学生做好体育考试项目的选考工作,某校统计了本县上届九年级毕业生体育考试各个项目参加的男、女生人数及平均成绩,并绘制成如图两个统计图,请结合统计图信息解决问题.
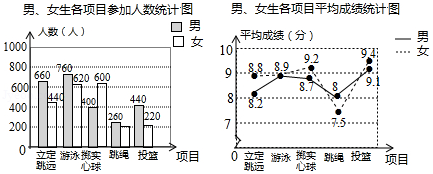
(1)“掷实心球”项目男、女生总人数是“跳绳”项目男、女生总人数的2倍,求“跳绳”项目的女生人数;
(2)若一个考试项目的男、女生总平均成绩不小于9分为“优秀”,试判断该县上届毕业生的考试项目中达到“优秀”的有哪些项目,并说明理由;
(3)请结合统计图信息和实际情况,给该校九年级学生体育考试项目的选择提出合理化建议.
数学拓展课程《玩转学具》课堂中,小陆同学发现:一副三角板中,含 的三角板的斜边与含 的三角板的长直角边相等,于是,小陆同学提出一个问题:如图,将一副三角板直角顶点重合拼放在一起,点 , , 在同一直线上,若 ,求 的长.
请你运用所学的数学知识解决这个问题.

如图1,地面 上两根等长立柱 , 之间悬挂一根近似成抛物线 的绳子.

(1)求绳子最低点离地面的距离;
(2)因实际需要,在离 为3米的位置处用一根立柱 撑起绳子(如图 ,使左边抛物线 的最低点距 为1米,离地面1.8米,求 的长;
(3)将立柱 的长度提升为3米,通过调整 的位置,使抛物线 对应函数的二次项系数始终为 ,设 离 的距离为 ,抛物线 的顶点离地面距离为 ,当 时,求 的取值范围.
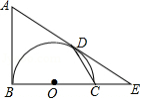
如图, 是以 为直径的半圆 的切线, 为半圆上一点, , , 的延长线相交于点 .
(1)求证: 是半圆 的切线;
(2)连接 ,求证: ;
(3)若 , ,求 的长.
2016年3月27日“丽水半程马拉松竞赛”在莲都举行,某运动员从起点万地广场西门出发,途经紫金大桥,沿比赛路线跑回终点万地广场西门.设该运动员离开起点的路程 (千米)与跑步时间 (分钟)之间的函数关系如图所示,其中从起点到紫金大桥的平均速度是0.3千米 分,用时35分钟,根据图象提供的信息,解答下列问题:
(1)求图中 的值;
(2)组委会在距离起点2.1千米处设立一个拍摄点 ,该运动员从第一次经过 点到第二次经过 点所用的时间为68分钟.
①求 所在直线的函数解析式;
②该运动员跑完赛程用时多少分钟?
试题篮
()