小明调查了本班每位同学最喜欢的颜色,并绘制了不完整的扇形图1及条形图2(柱的高度从高到低排列).条形图不小心被撕了一块,图2中" "应填的颜色是

| A. |
蓝 |
B. |
粉 |
C. |
黄 |
D. |
红 |
定理:三角形的一个外角等于与它不相邻的两个内角的和.
已知:如图, 是 的外角.求证: .
|
证法1:如图, (三角形内角和定理), 又 (平角定义), (等量代换). (等式性质). |
|
证法2:如图, , , 且 (量角器测量所得) 又 (计算所得) (等量代换). |
下列说法正确的是

| A. |
证法1还需证明其他形状的三角形,该定理的证明才完整 |
| B. |
证法1用严谨的推理证明了该定理 |
| C. |
证法2用特殊到一般法证明了该定理 |
| D. |
证法2只要测量够一百个三角形进行验证,就能证明该定理 |
如图,将数轴上 与6两点间的线段六等分,这五个等分点所对应数依次为 , , , , ,则下列正确的是

| A. |
|
B. |
|
| C. |
|
D. |
|
如图,在 中, , , ,按下列步骤作图:
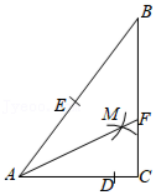
步骤1:以点 为圆心,小于 的长为半径作弧分别交 、 于点 、 .
步骤2:分别以点 、 为圆心,大于 的长为半径作弧,两弧交于点 .
步骤3:作射线 交 于点 .则 的长为
| A. |
6 |
B. |
|
C. |
|
D. |
|
如图,在边长为2的正方形 中,若将 绕点 逆时针旋转 ,使点 落在点 的位置,连接 ,过点 作 ,交 的延长线于点 ,则 的长为

| A. |
|
B. |
|
C. |
|
D. |
|
已知直线 与 轴、 轴分别交于 、 两点,点 是第一象限内的点,若 为等腰直角三角形,则点 的坐标为
| A. |
|
| B. |
或 |
| C. |
或 或 |
| D. |
或 或 或 |
图(1),在 中, ,点 从点 出发,沿三角形的边以 秒的速度逆时针运动一周,图(2)是点 运动时,线段 的长度 随运动时间 (秒 变化的关系图象,则图(2)中 点的坐标是

| A. |
|
B. |
|
C. |
|
D. |
|
一个四边形顺次添加下列条件中的三个条件便得到正方形:
.两组对边分别相等
.一组对边平行且相等
.一组邻边相等
.一个角是直角
顺次添加的条件:① ② ③
则正确的是

| A. |
仅① |
B. |
仅③ |
C. |
①② |
D. |
②③ |
学习圆的性质后,小铭与小熹就讨论起来,小铭说:"被直径平分的弦也与直径垂直",小熹说:"用反例就能说明这是假命题".下列判断正确的是
| A. |
两人说的都对 |
| B. |
小铭说的对,小熹说的反例不存在 |
| C. |
两人说的都不对 |
| D. |
小铭说的不对,小熹说的反例存在 |
如图所示,点 , , 对应的刻度分别为1,3,5,将线段 绕点 按顺时针方向旋转,当点 首次落在矩形 的边 上时,记为点 ,则此时线段 扫过的图形的面积为

| A. |
|
B. |
6 |
C. |
|
D. |
|
如 ,2, ,我们叫集合 ,其中1,2, 叫做集合 的元素.集合中的元素具有确定性(如 必然存在),互异性(如 , ,无序性(即改变元素的顺序,集合不变).若集合 ,1, ,我们说 .已知集合 ,0, ,集合 , , ,若 ,则 的值是
| A. |
|
B. |
0 |
C. |
1 |
D. |
2 |
如图,在 中, , ,点 在 上, ,以 为半径的 与 相切于点 ,交 于点 ,则 的长为
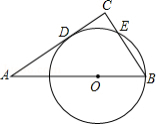
| A. |
|
B. |
|
C. |
|
D. |
1 |
试题篮
()