农历九月初九为中国传统的重阳节，倡导全社会树立尊老、敬老、爱老、助老的风气，为体现社会对老人的爱护，重阳节这一天上午，出租车司机小王在东西方向的公路上免费接送老人．如果规定向东为正，向西为负，出租车的行程如下（单位：千米）：
+15，﹣4，+13，﹣10，﹣12，+3，﹣13，﹣17．
（1）出车地记为0，最后一名老人送到目的地时，小王距出车地点的距离是多少？
（2）若汽车耗油量为0.1升/千米，这天上午汽车共耗油多少升？
如图，在四边形ABCD中，AD∥BC，∠C＝90°，BC＝16，DC＝12，AD＝21．动点P从点D出发，沿射线DA的方向以每秒2两个单位长的速度运动，动点Q从点C出发，在线段CB上以每秒1个单位长的速度向点B运动，点P，Q分别从点D，C同时出发，当点Q运动到点B时，点P随之停止运动．设运动的时间为t（秒）．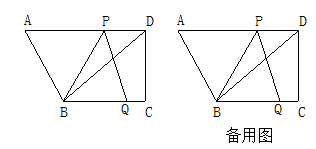
（1）请直接写出BD＝ ；AB＝ ；
（2）当t为何值时，以B，P，Q为顶点的三角形是等腰三角形？（求出一种得4分）
（3）是否存在时刻t，使得点P、Q关于BD对称，若存在，请你直接写出t的值，若不存在，请说明理由．
（本题8分）
（1） 求出下列各数：① 2的平方根； ②-27的立方根； ③
的算术平方根．
（2） 将（1）中求出的每个数准确地表示在数轴上．
（3） 将（1）中求出的每个数按从小到大的顺序排列，并用“﹤”连接．
把下列各数填在相应的大括号里：
，
，0．275，2，0，
，
，
，
，
（1）正整数集合：
；
（2）负整数集合：；
（3）正分数集合：；
（4）负分数集合：；
（5）整数集合：；
（本题10分）如图，数轴上的三点A、B、C分别表示有理数a、b、c．（O为原点）
（1）a－b 0，a＋c 0，b－c 0．
（用“＜”或“＞”或“=”号填空）
化简：|a－b|－|a＋c|＋|b－c|
（2）若数轴上两点A、B对应的数分别为－3、－1，点P为数轴上一动点，其对应的数为x．
①若点P到点A、点B的距离相等，则点P对应的数x为 ；
②若点A、点B分别以2个单位长度/秒和0．5个单位长度/秒的速度同时向右运动，点P以6个单位长度/秒的速度同时从原点O向左运动．当点A与点B之间的距离为1个单位长度时，求点P所对应的数x是多少？
已知：如图1，在△ABC中，A、B、C的坐标分别为（1,0），（4,0），（0,2），点M为边BC上的中点，点N为边AB 上一点，且N的横坐标为方程2n２＋5n－12＝0一个根，
（1）求N的坐标和直线MN的解析式 ；（3+3）
（2）判断直线MN与BC的位置关系，并说明你的理由；（1+3）
（3）如图2，①在图2中作出△ABC的外接圆；②过Q（
，0）作直线
⊥x轴，点P在直线上，且在第一象限，试确定一个点P，使得∠CPB+∠CAB=180°，求出满足条件的P点坐标．
为了节省材料，某水产养殖户利用水库的岸堤（岸堤足够长）为一边，用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域，而且这三块矩形区域的面积相等．设BC的长度为xm，矩形区域ABCD的面积为ym2．
（1）求AE的长（用x的代数式表示）
（2）当y=108m2时，求x的值
）阅读下面的材料，回答问题：
爱动脑筋的小明在学过用配方法解一元二次方程后，他发现二次三项式也可以配方，从而解决一些问题。例如：
-6x+10=（-6x+9-9）+10=
-9+10=+1≥1；因此-6x+10有最小值是1；
（1）尝试：-3-6x+5=-3（+2x+1-1）+5=-3
+8，因此-3-6x+5有最大值是______
（2）应用：有长为24米的篱笆，一面利用墙（墙的最大可用长度为a为15米），围成一个的长方形花圃。能围成面积最大的花圃吗？如果能，请求出最大面积．
如图，在△ABC中，∠CAB=90°，∠CBA=50°，以AB为直径作⊙O交BC于点D，点E在边AC上，且满足ED=EA．
（1）求∠DOA的度数；
（2）求证：直线ED与⊙O相切．
某商场要经营一种新上市的文具，进价为20元，试营销阶段发现：当销售单价是25元时，每天的销售量为250件，销售单价每上涨1元，每天的销售量就减少10件．
（1）写出商场销售这种文具，每天所得的销售利润
（元）与销售单价
（元）之间的函数关系式；
（2）求销售单价为多少元时，该文具每天的销售利润最大；最大值是多少？
试题篮
()
粤公网安备 44130202000953号
-4=0