初中数学解答题

图①②均为的正方形网格，点在格点上．

（1）在图①中确定格点，并画出以为顶点的四边形，使其为轴对称图形．（画出一个即可）
（2）在图②中确定格点，并画出以为顶点的四边形，使其为中心对称图形．（画出一个即可）

（本题满分14分，每小题各7分）按照要求的方法解一元二次方程
（1）3x²＋4x＋1＝0（配方法）；
（2）x²－1＝3x－3（因式分解法）．

如图所示，在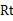△中，，，将绕点沿逆时针方向旋转得到．

（1）线段的长是 ，的度数是 ；
（2）连接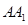，求证：四边形是平行四边形．

在数轴上标出下列各数：－1.5，2，+（-1），0，并用“＜”连接起来．

有20筐白菜，以每筐25千克为标准，超过或不足的部分别用正、负数来表示，记录如下：

（1）20筐白菜中，最重的一筐比最轻的一筐重多少千克？
（2）与标准质量比较，20筐白菜总计超过或不足多少千克？
（3）若白菜每千克售价为2．6元，出售这20筐白菜可得多少钱？

一名足球守门员练习折返跑，从守门员位置出发，向前记作正数，返回记作负数．他的记录如下（单位：m）．
+4，－3，+9，－7，－6，+11，－8
（1）守门员是否回到守门位置？
（2）守门员离开守门的位置最远是多少？
（3）守门员离开守门位置达7m以上（包括7m）的次数是多少？

（本题8分）宿豫区实验初中的图书室平均每天借出图书50册．如果某天借出53册，就记作+3；如果某天借出40册，就记作-10．上星期我校图书室借出图书记录如下：

（1）上星期五借出图书多少册？
（2）上星期二比上星期五多借出图书多少册？
（3）上星期总共借出图书多少册？

（本题8分）把下列各数分别填在相应的集合里．， ， ， ，， ， ， ， ， 0．101001， （每两个之间依次增加个）．
整数集合： ；
分数集合： ；
无理数集合： ；
负数集合： ．

已知点A在数轴上对应的数为a，点B对应的数为b，且，A、B之间的距离记作|AB|，
（1）求线段AB的长|AB|；
（2）设点P在数轴上对应的数为x，当|PA|－|PB|＝2时，求x的值；
（3）若点P在点A的左侧，M、N分别是PA、PB的中点，当点P在A的左侧移动时，下列两个结论：①|PM|＋|PN|的值不变；②|PN|－|PM|的值不变，其中只有一个结论正确，请判断出正确结论，并求其值．

一个三角形的第一条边长为（x＋2）cm，第二条边长比第一条边长小5cm，第三条边长是第二条边长的2倍．
（1）用含x的代数式表示这个三角形的周长；
（2）计算当x为6cm时这个三角形的周长．

（1）如图，两个圈分别表示负数集和分数集，请将﹣50%，2012，0.618，﹣3，，0，5.9，﹣3.14，﹣92中，符合要求的数填入相应的圈中；
（2）在数轴上表示下列四个数，，0，，并把它们用“＜”号连接起来．
（1）（2）

有理数a、b、c在数轴上的对应点如图所示：

化简代数式：．

化简：（1）
（2）

（本题14分）【问题探究】
（1）如图1，锐角△ABC中分别以AB、AC为边向外作等腰△ABE和等腰△ACD，使AE=AB，AD=AC，∠BAE=∠CAD，连接BD，CE，试猜想BD与CE的大小关系，并说明理由．
【深入探究】
（2）如图2，四边形ABCD中，AB=3cm，BC=1cm，∠ABC=∠ACD=∠ADC=45°，求BD的长（结果保留根号）．
（3）如图3，在（2）的条件下，当△ACD在线段AC的左侧时，求BD的长（结果保留根号）．

（本题12分）如图，有一个三角形ABC，三边为AC=6cm，BC=8cm，AB=10cm，沿AD折叠，使点C落在AB上的点E处，求线段CD的长．