初中数学解答题

解不等式，并把它的解集表示在数轴上．

解方程组．

先仔细阅读材料，再尝试解决问题：
完全平方公式x²±2xy+y²=（x±y）²及（x±y）²的值恒为非负数的特点在数学学习中有着广泛的应用，比如探求多项式2x²+12x﹣4的最大（小）值时，我们可以这样处理：
解：原式=2（x²+6x﹣2）
=2（x²+6x+9﹣9﹣2）
=2[（x+3）²﹣11]
=2（x+3）²﹣22
因为无论x取什么数，都有（x+3）²的值为非负数
所以（x+3）²的最小值为0，此时x=﹣3
进而2（x+3）²﹣22
的最小值是2×0﹣22=﹣22
所以当x=﹣3时，原多项式的最小值是﹣22
解决问题：
请根据上面的解题思路，探求多项式3x²﹣6x+12的最小值是多少，并写出对应的x的取值．

解方程组：
①②．

将下列多项式分解因式：
①2x²﹣4xy+2y²
②x³y﹣9xy³．

已知直线l为x+y=8，点P（x，y）在l上，且x＞0，y＞0，点A的坐标为（6，0）．

（1）设△OPA的面积为S，求S与x的函数关系式，并直接写出x的取值范围；
（2）当S=9时，求点P的坐标；
（3）在直线l上有一点M，使OM+MA的和最小，求点M的坐标．

已知▱ABCD中，AE平分∠BAD，CF平分∠BCD，分别交CD、AB于E、F，求证：AE=CF．

滨湖区举行“我的中国梦”演讲比赛，某校中学组根据初赛成绩在七2014-2015学年八年级分别选出10名同学参加比赛，这些选手的决赛成绩如图所示：

（1）请你把下面的表格填写完整：

（2）考虑平均数与方差，你认为哪个年级的团体成绩更好些；
（3）假设在每个年级的选手中分别选出3人参加总决赛，你认为哪个年级的实力更强一些，请说明理由．

如图，已知△ABC中，AB=AC，E，D，F分别是边AB，BC，AC的中点．

（1）求证：四边形AEDF是菱形；
（2）若∠B=30°，BC=4，求四边形AEDF的周长．

（1）
（2）．

先化简，再求值：，其中x=1+，y=1﹣．

某校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查，得到一组学生捐款情况的数据，根据这组数据绘制成如图所示的统计图．

（1）这一组学生平均每人捐款多少元？
（2）这组数据的众数是20 ，中位数是14.5 ；
（3）请估计该校2000名学生中捐款为20元的人数．

在“母亲节”期间，某校部分团员准备购进一批“康乃馨”进行销售，并将所得利润捐给贫困同学的母亲．根据市场调查，这种“康乃馨”的销售量y（枝）与销售单价x（元/枝）之间成一次函数关系，它的部分图象如图．

（1）试求y与x之间的函数关系式；
（2）若“康乃馨”的进价为5元/枝，且要求每枝的销售盈利不少于1元，问：在此次活动中，他们最多可购进多少数量的康乃馨？

“最美女教师”张丽莉，为抢救两名学生，以致双腿高位截肢，社会各界纷纷为她捐款，我市某中学九年级一班全体同学参加了捐款活动，该班同学捐款情况的部分统计图如图所示：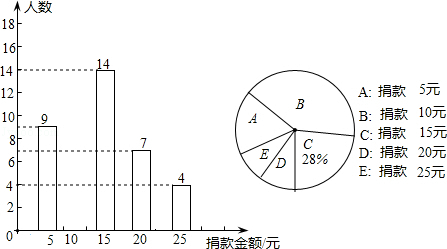

（1）求该班的总人数；
（2）将条形图补充完整，并写出捐款总额的众数；
（3）该班平均每人捐款多少元？

某单位准备印刷一批书面材料，现有两个印刷厂可供选择，甲厂的费用分为制作费和印刷费两部分，乙厂直接按印刷数量收取印刷费．甲厂的费用y（千元）与书面材料数量x（千份）的关系见表：

书面材料数量x（千份）	0	1	2	3	4	5	6	.........
甲厂的印刷费用y（千元）	1	1.5	2	2.5	3	3.5	4	.........

乙厂的印刷费用y（千元）与书面材料数量x（千份）的函数关系图象如图所示．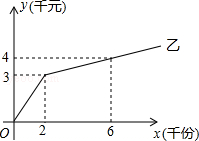

（1）请你写出甲厂的费用y与x的函数解析式，并在图中坐标系中画出甲厂的费用y与x的函数图象．
（2）请写出乙厂费用y与x的函数解析式，试求出当x在什么范围内时乙厂比甲厂的费用低？
（3）现有一客户需要印10千份书面材料，请问你如果是客户你如何选择？