初中数学解答题

解方程：．

化简或求值
（1）
（2），其中a=﹣，b=1．

某公司招聘职员，对甲、乙两位候选人进行了面试和笔试，面试中包括形体和口才，笔试中包括专业水平和创新能力考察，他们的成绩（百分制）如下表：

候选人	面试	笔试
	形体	口才	专业水平	创新能力
甲	86	90	96	92
乙	92	88	95	93

（1）若公司根据经营性质和岗位要求认为：形体、口才、专业水平、创新能力按照4：6：5：5的比确定，请计算甲、乙两人各自的平均成绩，看看谁将被录取？
（2）若公司根据经营性质和岗位要求认为：面试成绩中形体占15%，口才占20%，笔试成绩中专业水平占40%，创新能力占25%，那么你认为该公司应该录取谁．

如图，在四边形ABCD中，∠B=∠D，∠1=∠2，求证：四边形ABCD是平行四边形．

如图是一种儿童的游乐设施﹣儿童荡板．小明想验证这个荡板上方的四边形是否是平行四边形，现在手头只有一根足够长的绳子，请你帮助他设计一个验证方案，并说明理由．

广安市积极开展“阳光体育进校园”活动，各校学生坚持每天锻炼一小时．某校根据实际，决定主要开设A：乒乓球，B：篮球，C：跑步，D：跳绳四种运动项目．为了解学生最喜欢哪一种项目，随机抽取了部分学生进行调查，并将调查结果绘制成如下统计图．请你结合图中信息解答下列问题．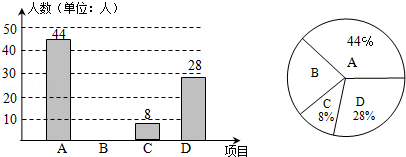

（1）样本中最喜欢B项目的人数百分比是________，其所在扇形图中的圆心角的度数是____；
（2）请把统计图补充完整；
（3）已知该校有1200人，请根据样本估计全校最喜欢乒乓球的人数是多少？

如图，已知∠1=∠2，∠C=∠D，

求证：∠A=∠F．

（1）解不等式：﹣＞﹣2，并把解集在数轴上表示出来．
（2）解不等式组：，并将不等式组的解集在所给数轴上表示出来．

先化简再求值：（）÷（x-1），其中x=．

解方程组．

如图，CD为⊙O的直径，点B在⊙O上，连接BC、BD，过点B的切线AE与CD的延长线交于点A，OE∥BD，交BC于点F，交AE于点E．

（1）求证：∠E=∠C；
（2）当⊙O的半径为3，tanC=时，求BE的长．

小明为了了解本班全体同学在阅读方面的情况，采取全面调查的方法，从喜欢阅读“科普常识、小说、漫画、营养美食”等四类图书中调查了全班学生的阅读情况（要求每位学生只能选择一种自己喜欢阅读的图书类型）根据调查的结果绘制了下面两幅不完整的统计图．

请你根据图中提供的信息解答下列问题：
（1）该班的学生人数为 人，并把条形统计图补充完整；
（2）在扇形统计图中，表示“漫画”类所对圆心角是 度，喜欢阅读“营养美食”类图书的人数占全班人数的百分比为 ；
（3）如果喜欢阅读“营养美食”类图书的4名学生中有3名男学生和1名女学生，现在打算从中随机选出2名学生参加学校组织的“营养美食”知识大赛，请用列表或画树状图的方法，求选出的2名学生中恰好有1名男生和1名女生的概率．

如图，矩形ABCD，E是AB上一点，且DE=AB，过C作CF⊥DE于F．

（1）猜想：AD与CF的大小关系；
（2）请证明上面的结论．

解方程组：．

解分式方程：．