在一个不透明的袋子中装有4个红球和2个白球,这些球除了颜色外无其他差别,从袋子中随机摸出一个球,则摸出白球的概率是 .
已知抛物线 与 轴交于 , 两点(点 在点 的左侧),将这条抛物线向右平移 个单位,平移后的抛物线与 轴交于 , 两点(点 在点 的左侧),若 , 是线段 的三等分点,则 的值为 .
在如图所示的平行四边形 中, , ,将 沿对角线 折叠,点 落在 所在平面内的点 处,且 过 的中点 ,则 的周长等于 .

将从1开始的连续自然数按以下规律排列:
|
第1行 |
1 |
||||||||
|
第2行 |
2 |
3 |
4 |
||||||
|
第3行 |
9 |
8 |
7 |
6 |
5 |
||||
|
第4行 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
||
|
第5行 |
25 |
24 |
23 |
22 |
21 |
20 |
19 |
18 |
17 |
则2018在第 行.
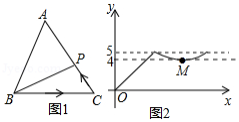
如图1,点 从 的顶点 出发,沿 匀速运动到点 ,图2是点 运动时,线段 的长度 随时间 变化的关系图象,其中 为曲线部分的最低点,则 的面积是 .
如图,在正方形 中, ,把边 绕点 逆时针旋转 得到线段 ,连接 并延长交 于点 ,连接 ,则三角形 的面积为 .

我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为 , , ,则该三角形的面积为 .现已知 的三边长分别为1,2, ,则 的面积为 .

如图,某商店营业大厅自动扶梯 的倾斜角为 , 的长为12米,则大厅两层之间的高度为 米.(结果保留两个有效数字)【参考数据; sin 31 ° = 0 . 515 , cos 31 ° = 0 . 857 , tan 31 ° = 0 . 601 】

如图,点 为正六边形 的中心,点 为 中点,以点 为圆心,以 的长为半径画弧得到扇形 ,点 在 上;以点 为圆心,以 的长为半径画弧得到扇形 ,把扇形 的两条半径 , 重合,围成圆锥,将此圆锥的底面半径记为 ;将扇形 以同样方法围成的圆锥的底面半径记为 ,则 .
试题篮
()